Η μικρή ιστορία του προβλήματος : Υπάρχει άσκηση στο σχολικό που ζητά τα αποδειχθεί ότι το εμβαδόν του τριγώνου
που σχηματίζει μια εφαπτομένη της καμπύλης

με τους άξονες ισούται με

. Γενικεύοντας
για την

, προκύπτει :

. Για να γίνει το αποτέλεσμα πιο "φανταιζί" έκοψα στην μέση το εμβαδόν ,
οπότε τώρα :

. Μου δημιουργήθηκε η απορία αν υπάρχουν άλλες τέτοιες συναρτήσεις .
Η αρχική μου "πρόβλεψη" ήταν : μάλλον ναι . Διαβάζοντας την - τρομερή κατά τα άλλα

- λύση του Ευάγγελου
ένοιωσα την ικανοποίηση για την δύναμη του θέματος αλλά και την διάψευση της αρχικής μου προσδοκίας .
Η παρέμβαση όμως του Σταύρου

, ήταν θείο δώρο : Βρέθηκαν κι άλλες λύσεις !
Η αρχική συνάρτηση ήταν η
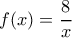
, (

) . Θέτοντας τώρα

,

- Η άλλη λύση.png (11.16 KiB) Προβλήθηκε 665 φορές
προκύπτει η :

, η οποία έχει επίσης αυτήν την ιδιότητα και μάλιστα
χωρίς περιορισμό στο πεδίο ορισμού . Νομίζω κύριοι ότι κάναμε σπουδαία δουλειά ...
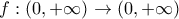 . Σε σημείο
. Σε σημείο  , το οποίο κινείται επί της
, το οποίο κινείται επί της  φέρω
φέρω  στο σημείο
στο σημείο  . Αν το εμβαδόν του τριγώνου
. Αν το εμβαδόν του τριγώνου 
 ) : α) Βρείτε ( ακριβέστερα μαντέψτε ) μία
) : α) Βρείτε ( ακριβέστερα μαντέψτε ) μία  μ' αυτήν την ιδιότητα .
μ' αυτήν την ιδιότητα . , που έχουν αυτήν την ιδιότητα ;
, που έχουν αυτήν την ιδιότητα ;
 και το σταθερό εμβαδόν είναι
και το σταθερό εμβαδόν είναι 
 , η εξίσωση της εφαπτομένης είναι η
, η εξίσωση της εφαπτομένης είναι η  , οπότε για την τετμημένη του
, οπότε για την τετμημένη του  . Αν
. Αν  , τότε
, τότε  , άτοπο, οπότε
, άτοπο, οπότε  (και μάλιστα
(και μάλιστα  ) και
) και 
 και το ύψος του τριγώνου αν πάρω σαν βάση την
και το ύψος του τριγώνου αν πάρω σαν βάση την  είναι το
είναι το 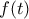 . Έτσι, για κάθε
. Έτσι, για κάθε 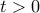 έχουμε ότι
έχουμε ότι 
 ή ισοδύναμα
ή ισοδύναμα 
 ώστε
ώστε  απ΄όπου συνεπάγεται
απ΄όπου συνεπάγεται  .
. 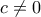 . Έστω
. Έστω  είναι ρίζα του τριωνύμου
είναι ρίζα του τριωνύμου  , οπότε
, οπότε 
 και έπεται ότι
και έπεται ότι  .
. ;
; και επειδή
και επειδή 

 με τους άξονες ισούται με
με τους άξονες ισούται με  . Γενικεύοντας
. Γενικεύοντας , προκύπτει :
, προκύπτει :  . Για να γίνει το αποτέλεσμα πιο "φανταιζί" έκοψα στην μέση το εμβαδόν ,
. Για να γίνει το αποτέλεσμα πιο "φανταιζί" έκοψα στην μέση το εμβαδόν ,  . Μου δημιουργήθηκε η απορία αν υπάρχουν άλλες τέτοιες συναρτήσεις .
. Μου δημιουργήθηκε η απορία αν υπάρχουν άλλες τέτοιες συναρτήσεις .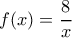 , (
, (  ) . Θέτοντας τώρα
) . Θέτοντας τώρα  ,
,  , η οποία έχει επίσης αυτήν την ιδιότητα και μάλιστα
, η οποία έχει επίσης αυτήν την ιδιότητα και μάλιστα