Mihalis_Lambrou έγραψε: ↑Κυρ Ιουν 07, 2020 9:50 am
Χωρίς βλάβη το

περιέχει μη φραγμένη ακολουθία

από θέσεις τοπικών ακροτάτων. Η συνεχής

σε κάθε ένα από τα διαστήματα
![[a_n, a_{n+1}] [a_n, a_{n+1}]](/forum/ext/geomar/texintegr/latexrender/pictures/a135e5246ef1a86772fae919cc704e1a.png)
περιέχει σημείο

όπου η συνάρτηση (περιορισμένη σε αυτό το διάστημα) έχει θέση ολικού ελαχίστου. Όμοια, περιέχει σημείο

όπου η συνάρτηση έχει θέση ολικού μεγίστου. Με άλλα λόγια στο εν λόγω διάστημα ισχύει
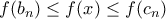
. Υπόψη ότι τα

ανήκουν στο

.
Έστω τώρα

. Αφού

, υπάρχει

τέτοιο ώστε για κάθε

ισχύει
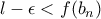
και

. Για

ισχύει: Για κάποιο

έχουμε
![x\in [a_m,a_{m+1}] x\in [a_m,a_{m+1}]](/forum/ext/geomar/texintegr/latexrender/pictures/b5a3f98c8cb499b5405b1db182495e1c.png)
και άρα

. Όμοια

. Τα δύο μαζί δείχνουν ότι

.
Στην απόδειξη, στην ουσία, χρησιμοποιήσαμε ότι η

παίρνει μέγιστη και ελάχιστη τιμή στα συμπαγή υποσύνολα του
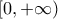
που είναι κάπως ασθενέστερη υπόθεση της συνέχειας - π.χ. η

. Βέβαια, το συγκεκριμένο παράδειγμα είναι μία συνάρτηση σχεδόν παντού ίση με μία συνεχή συνάρτηση. Δεν ξέρω αν ισχύει και το ακόλουθο:
Μία συνάρτηση που παίρνει μέγιστη και ελάχιστη τιμή σε κάθε συμπαγές υποσύνολο των πραγματικών είναι σχεδόν παντού ίση με μία συνεχή.
Όπως το σκέφτομαι τώρα, βασικά, θα μπορούσαμε να πάρουμε διαμερίσεις του

της μορφής

και να φτιάξουμε μία ακολουθία συνεχών συναρτήσεων

που σε κάθε διάστημα

να διέρχεται από τα σημεία μεγίστου και ελαχίστου της

. Τώρα, το αν η ακολουθία αυτή είναι ομοιόμορφα βασικά και οι ουσιώδεις λεπτομέρειες που μας λείπουν είναι πράγματα που δεν προλαβαίνω να σκεφτώ τώρα.
Ίσως όμως αργότερα.
 η οποία είναι ορισμένη στο
η οποία είναι ορισμένη στο 
 το σύνολο των θέσεων τοπικών ακροτάτων της
το σύνολο των θέσεων τοπικών ακροτάτων της  . Υποθέτουμε ότι το
. Υποθέτουμε ότι το  δεν είναι
δεν είναι  με
με  για κάθε
για κάθε  και
και 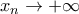
 , να δείξετε ότι
, να δείξετε ότι 

![f(x)=x-[x], \, x\ge 0, f(x)=x-[x], \, x\ge 0,](/forum/ext/geomar/texintegr/latexrender/pictures/9f61569740cf7901694ec8d3d806aa3b.png) έχει τοπικά ελάχιστα ακριβώς
έχει τοπικά ελάχιστα ακριβώς  . Δεν έχει τοπικά μέγιστα. Έτσι, για οποιαδήποτε ακολουθία
. Δεν έχει τοπικά μέγιστα. Έτσι, για οποιαδήποτε ακολουθία  , πλην όμως
, πλην όμως 
 από θέσεις τοπικών ακροτάτων. Η συνεχής
από θέσεις τοπικών ακροτάτων. Η συνεχής ![[a_n, a_{n+1}] [a_n, a_{n+1}]](/forum/ext/geomar/texintegr/latexrender/pictures/a135e5246ef1a86772fae919cc704e1a.png) περιέχει σημείο
περιέχει σημείο  όπου η συνάρτηση (περιορισμένη σε αυτό το διάστημα) έχει θέση ολικού ελαχίστου. Όμοια, περιέχει σημείο
όπου η συνάρτηση (περιορισμένη σε αυτό το διάστημα) έχει θέση ολικού ελαχίστου. Όμοια, περιέχει σημείο  όπου η συνάρτηση έχει θέση ολικού μεγίστου. Με άλλα λόγια στο εν λόγω διάστημα ισχύει
όπου η συνάρτηση έχει θέση ολικού μεγίστου. Με άλλα λόγια στο εν λόγω διάστημα ισχύει 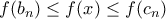 . Υπόψη ότι τα
. Υπόψη ότι τα  ανήκουν στο
ανήκουν στο  . Αφού
. Αφού  , υπάρχει
, υπάρχει  τέτοιο ώστε για κάθε
τέτοιο ώστε για κάθε  ισχύει
ισχύει 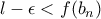 και
και  . Για
. Για  ισχύει: Για κάποιο
ισχύει: Για κάποιο  έχουμε
έχουμε ![x\in [a_m,a_{m+1}] x\in [a_m,a_{m+1}]](/forum/ext/geomar/texintegr/latexrender/pictures/b5a3f98c8cb499b5405b1db182495e1c.png) και άρα
και άρα  . Όμοια
. Όμοια  . Τα δύο μαζί δείχνουν ότι
. Τα δύο μαζί δείχνουν ότι  .
.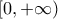 που είναι κάπως ασθενέστερη υπόθεση της συνέχειας - π.χ. η
που είναι κάπως ασθενέστερη υπόθεση της συνέχειας - π.χ. η  . Βέβαια, το συγκεκριμένο παράδειγμα είναι μία συνάρτηση σχεδόν παντού ίση με μία συνεχή συνάρτηση. Δεν ξέρω αν ισχύει και το ακόλουθο:
. Βέβαια, το συγκεκριμένο παράδειγμα είναι μία συνάρτηση σχεδόν παντού ίση με μία συνεχή συνάρτηση. Δεν ξέρω αν ισχύει και το ακόλουθο: της μορφής
της μορφής  και να φτιάξουμε μία ακολουθία συνεχών συναρτήσεων
και να φτιάξουμε μία ακολουθία συνεχών συναρτήσεων  που σε κάθε διάστημα
που σε κάθε διάστημα  να διέρχεται από τα σημεία μεγίστου και ελαχίστου της
να διέρχεται από τα σημεία μεγίστου και ελαχίστου της 
 μετρήσιμο με την ιδιότητα.
μετρήσιμο με την ιδιότητα. να έχουν με κάθε διάστημα τομή με θετικό μέτρο.
να έχουν με κάθε διάστημα τομή με θετικό μέτρο.
