viewtopic.php?f=56&t=3390
του Peter
Αλλαξα φάκελο γιατί η λύση που έχω είναι σε αυτόν
Άσκηση 1. Εξετάστε αν υπάρχει
 με την ιδιότητα:
με την ιδιότητα:  για κάθε
για κάθε  .
.Συντονιστής: emouroukos
 με την ιδιότητα:
με την ιδιότητα:  για κάθε
για κάθε  .
. είναι γνησίως αύξουσα αφού αν
είναι γνησίως αύξουσα αφού αν  τότε (με
τότε (με  ) έχουμε
) έχουμε
 για κάθε
για κάθε  . Σε διαφορετική περίπτωση υπάρχει
. Σε διαφορετική περίπτωση υπάρχει  και
και  ώστε
ώστε  . Τότε όμως είναι:
. Τότε όμως είναι:
 . Αυτό αποδεικνύεται εύκολα επαγωγικά αφού είναι αληθές για
. Αυτό αποδεικνύεται εύκολα επαγωγικά αφού είναι αληθές για  και στο επαγωγικό βήμα παίρνουμε:
και στο επαγωγικό βήμα παίρνουμε:
 αρκετά μεγάλο θα έχουμε
αρκετά μεγάλο θα έχουμε 
 με θετικό συντελεστή του
με θετικό συντελεστή του  .)
.)


 παίρνουμε
παίρνουμε

 ωστε
ωστε


 και
και  δίνει
δίνει 
Μέχρι εδώ τα ίδια. Είναι εύκολο να δείξουμε ότι
 (το όριο υπάρχει από μονοτονία).
(το όριο υπάρχει από μονοτονία). θα είναι (
θα είναι ( σταθερό)
σταθερό)  (άτοπο).
(άτοπο). Για τυχόν
Για τυχόν  θα υπάρχει
θα υπάρχει 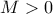 ώστε
ώστε  .
.  και
και  είναι ολοκληρώσιμες ως μονότονες οπότε για
είναι ολοκληρώσιμες ως μονότονες οπότε για  έχουμε
έχουμε


 για κάθε
για κάθε  αν πάρουμε
αν πάρουμε  και
και  αρκετά μεγάλο.
αρκετά μεγάλο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες