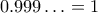 . Στην αρχή είπα να τους θυμίσω την απόδειξη που έχει στα βιβλία του γυμνασίου, που, γενικά, δε θεωρώ ότι έχει κάποια διδακτική αξία (ή, ενδεχομένως, δεν έχω δει εγώ ακόμα τη διδακτική αξία της):
. Στην αρχή είπα να τους θυμίσω την απόδειξη που έχει στα βιβλία του γυμνασίου, που, γενικά, δε θεωρώ ότι έχει κάποια διδακτική αξία (ή, ενδεχομένως, δεν έχω δει εγώ ακόμα τη διδακτική αξία της):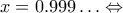




Ωστόσο, η απόπειρα αυτή έπεσε στο κενό, μιας και μου ζήτησαν μια εξήγηση που να μην μοιάζει με τέχνασμα (όχι ότι είχαν και άδικο, εδώ που τα λέμε).
Έτσι, έκανα την εξής απόπειρα. Θεωρούμε τους αριθμούς
 για τους οποίους εύκολα βλέπουμε ότι
για τους οποίους εύκολα βλέπουμε ότι  και, υποθέτουμε, ότι
και, υποθέτουμε, ότι  (το να είναι μεγαλύτερο το απορρίπτουν και οι μαθητές διαισθητικά). Τότε, οι δύο αριθμοί, 1 και
(το να είναι μεγαλύτερο το απορρίπτουν και οι μαθητές διαισθητικά). Τότε, οι δύο αριθμοί, 1 και  , έχουν κάποια απόσταση, αφού
, έχουν κάποια απόσταση, αφού  . Έπειτα από λίγη κουβέντα συμφωνήσαμε ότι μπορούμε να βρούμε έναν αριθμό της μορφής
. Έπειτα από λίγη κουβέντα συμφωνήσαμε ότι μπορούμε να βρούμε έναν αριθμό της μορφής  , για κάποιο
, για κάποιο  τέτοιον ώστε
τέτοιον ώστε  . Όμως, ισχύει και το εξής:
. Όμως, ισχύει και το εξής:
οπότε και βλέπουμε ότι, για το εν λόγω
 έχουμε
έχουμε  , άτοπο.
, άτοπο.Από αυτήν την προσέγγιση πείστηκε (και εντυπωσιάστηκε) η μαθήτρια που, κατ' εμέ, είχε την καλύτερη διαίσθηση και μαθηματική παιδεία στο τμήμα. Αλλά οι υπόλοιποι, λίγο έως πολύ, δεν έδειχναν και πολύ πεπεισμένοι.
Έπειτα, δοκίμασα και το εξής (η κουβέντα έγινε μετά τη λήξη του μαθήματος, οπότε δεν είχαμε ιδιαίτερο θέμα χρόνου). Έγραψα έναν από τους αριθμούς
 στη μορφή (μετά από πράξεις και χωρίς το σύμβολο του αθροίσματος):
στη μορφή (μετά από πράξεις και χωρίς το σύμβολο του αθροίσματος):
Το οποίο από τον τύπο για το άθροισμα όρων γεωμετρικής προόδου είναι ίσο με:

Επίσης, σχετικά εύκολα, καταλήξαμε στο συμπέρασμα ότι ο αριθμός
 θα γράφεται στη μορφή (πάντα, όχι με σύμβολο άθροισης αλλά με τελίτσες να υπονοούν την ύπαρξη άπειρων όρων):
θα γράφεται στη μορφή (πάντα, όχι με σύμβολο άθροισης αλλά με τελίτσες να υπονοούν την ύπαρξη άπειρων όρων):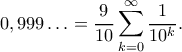
Τώρα, το πεπερασμένο άθροισμα, για μεγάλα
 , θα προσεγγίζει το μικρό, οπότε, παίρνοντας το
, θα προσεγγίζει το μικρό, οπότε, παίρνοντας το  μεγάλο έχουμε και πάλι το ζητούμενο.
μεγάλο έχουμε και πάλι το ζητούμενο.Παράλληλα, είχαμε και ένα σχήμα για να τα βλέπουμε γραφικά (ένα τετράγωνο χωρισμένο σε 10 μέρη από τα οποία χρωματίσαμε τα 9 και αυτό που απέμεινε το χωρίσαμε σε 10 μέρη και χρωματίσαμε τα 9 κ.ο.κ.). Ενώ, με τα τελευταία, κάποιοι μαθητές πείστηκαν, σχετικά, έμεινα μία διάχυτη εντύπωση σε ορισμένους (τους, ομολογουμένως, πιο αδύναμους) ότι το
 δεν είναι ποτέ ίσο με 1 αλλά πλησιάζει στο ένα (με άλλα λόγια, ταυτίστηκε με την ακολουθία και όχι με το όριο).
δεν είναι ποτέ ίσο με 1 αλλά πλησιάζει στο ένα (με άλλα λόγια, ταυτίστηκε με την ακολουθία και όχι με το όριο).Τι άλλο θα μπορούσε κανείς να πει ή πώς αλλιώς θα μπορούσε να παρουσιαστεί εξαρχής το ζήτημα για να αποφευχθεί αυτή η παρανόηση;


 .
.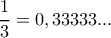 και πολλαπλασιασμό επί
και πολλαπλασιασμό επί  ) έχουν χιλιοειπωθεί και είναι γραμμένα σε πολλά σημεία.
) έχουν χιλιοειπωθεί και είναι γραμμένα σε πολλά σημεία.  ήταν αρκετά απλό και έξυπνο (αν και δεν ξέρω τι διαίσθηση παρέχει, είναι ωστόσο πιο πειστικό από την πρώτη απόδειξη). Επομένως, θα πρέπει πρώτα να ξανακοιτάξω τη σχετική βιβλιογραφία! Ευχαριστώ!
ήταν αρκετά απλό και έξυπνο (αν και δεν ξέρω τι διαίσθηση παρέχει, είναι ωστόσο πιο πειστικό από την πρώτη απόδειξη). Επομένως, θα πρέπει πρώτα να ξανακοιτάξω τη σχετική βιβλιογραφία! Ευχαριστώ! με την ιδιότητα να είναι όλα τους μεγαλύτερα από κάθε φυσικό αριθμό. Επομένως, πιστεύω, ότι την έννοια του
με την ιδιότητα να είναι όλα τους μεγαλύτερα από κάθε φυσικό αριθμό. Επομένως, πιστεύω, ότι την έννοια του 

 είναι ένας άπειρος ακέραιος. Ως εκ τούτου, το αποτέλεσμα είναι, σε όρους μη συμβατικής ανάλυσης, διαφορετικό του 1 (πράγματι, η διαφορά τους είναι ένα απειροστό, δηλαδή θετική και μικρότερη από κάθε θετικό πραγματικό αριθμό).
είναι ένας άπειρος ακέραιος. Ως εκ τούτου, το αποτέλεσμα είναι, σε όρους μη συμβατικής ανάλυσης, διαφορετικό του 1 (πράγματι, η διαφορά τους είναι ένα απειροστό, δηλαδή θετική και μικρότερη από κάθε θετικό πραγματικό αριθμό). :
:
 η θεωρία των πραγματικών αριθμών, δηλαδή όλες οι προτάσεις που μπορούν να αποδειχθούν από τα 13 πρώτα αξιώματα των πραγματικών αριθμών στην πρωτοβάθμια λογική. Το αξίωμα της πληρότητας είναι δευτεροβάθμιο (χρειάζεται ποσόδειξη σε σύνολα), ως εκ τούτου, δεν έχουμε το
η θεωρία των πραγματικών αριθμών, δηλαδή όλες οι προτάσεις που μπορούν να αποδειχθούν από τα 13 πρώτα αξιώματα των πραγματικών αριθμών στην πρωτοβάθμια λογική. Το αξίωμα της πληρότητας είναι δευτεροβάθμιο (χρειάζεται ποσόδειξη σε σύνολα), ως εκ τούτου, δεν έχουμε το  ως (το) πλήρες ολικά διατεταγμένο σώμα αλλά ως ένα ολικά διατεταγμένο σώμα. Χρησιμοποιώντας το
ως (το) πλήρες ολικά διατεταγμένο σώμα αλλά ως ένα ολικά διατεταγμένο σώμα. Χρησιμοποιώντας το  τέτοιο ώστε για κάθε θετικό πραγματικό αριθμό
τέτοιο ώστε για κάθε θετικό πραγματικό αριθμό  να ισχύει
να ισχύει  .
. .
. είναι απειροστός, τότε ο
είναι απειροστός, τότε ο  είναι άπειρος.
είναι άπειρος.



 είναι κάποιος άπειρος ακέραιος). Σε αυτόν τον συμβολισμό, το άθροισμα:
είναι κάποιος άπειρος ακέραιος). Σε αυτόν τον συμβολισμό, το άθροισμα: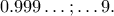
 οστό). Όμως, όπως είδαμε:
οστό). Όμως, όπως είδαμε: