![f, g: [0,1] \rightarrow R f, g: [0,1] \rightarrow R](/forum/ext/geomar/texintegr/latexrender/pictures/8b4bb07cb195fe0a9d71b065bdd99c53.png) με
με 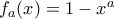 και
και  όπου
όπου 
(1) Να δείξετε ότι οι εξισώσεις
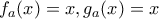 έχουν μοναδική λύση στο
έχουν μοναδική λύση στο  για κάθε
για κάθε 
(2) Αν με
 συμβολίσουμε τις ρίζες των
συμβολίσουμε τις ρίζες των 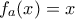 και
και 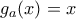 αντίστοιχα
αντίστοιχα να αποδείξετε ότι

Συντονιστής: emouroukos
![f, g: [0,1] \rightarrow R f, g: [0,1] \rightarrow R](/forum/ext/geomar/texintegr/latexrender/pictures/8b4bb07cb195fe0a9d71b065bdd99c53.png) με
με 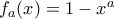 και
και  όπου
όπου 
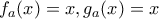 έχουν μοναδική λύση στο
έχουν μοναδική λύση στο  για κάθε
για κάθε 
 συμβολίσουμε τις ρίζες των
συμβολίσουμε τις ρίζες των 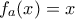 και
και 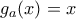 αντίστοιχα
αντίστοιχα 




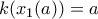 οπότε
οπότε 


Αλλιώς.Λάμπρος Κατσάπας έγραψε: ↑Κυρ Ιούλ 07, 2019 8:56 pmΔίνονται οι συναρτήσειςμε
και
όπου
(1) Να δείξετε ότι οι εξισώσειςέχουν μοναδική λύση στο
για κάθε
(2) Αν μεσυμβολίσουμε τις ρίζες των
και
αντίστοιχα
να αποδείξετε ότι
 , εύκολα βλέπουμε ότι έχουν αρνητική παράγωγο στο
, εύκολα βλέπουμε ότι έχουν αρνητική παράγωγο στο  , οπότε έχουν το πολύ μία ρίζα εκάστη. Επίσης αλλάζουν πρόσημο από
, οπότε έχουν το πολύ μία ρίζα εκάστη. Επίσης αλλάζουν πρόσημο από  στο
στο  , άρα έχουν τουλάχιστον μία ρίζα. Αυτό δείχνει το α) ερώτημα.
, άρα έχουν τουλάχιστον μία ρίζα. Αυτό δείχνει το α) ερώτημα.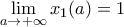 και
και 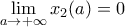 . Επίσης θα δείξουμε ότι ισχύει
. Επίσης θα δείξουμε ότι ισχύει  για κάθε
για κάθε  .
.  . Θέλουμε να δείξουμε ότι για μεγάλα
. Θέλουμε να δείξουμε ότι για μεγάλα  είναι
είναι 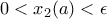 . Πράγματι, αφού
. Πράγματι, αφού  καθώς
καθώς  , από κάποιο σημείο και πέρα είναι
, από κάποιο σημείο και πέρα είναι 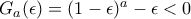 . Για τα ίδια αυτά
. Για τα ίδια αυτά  είναι
είναι  και άρα (αφού
και άρα (αφού  φθίνουσα), είναι
φθίνουσα), είναι  , όπως θέλαμε.
, όπως θέλαμε.  εργαζόμαστε όμοια ή, ακόμα καλύτερα, έχουμε
εργαζόμαστε όμοια ή, ακόμα καλύτερα, έχουμε  . Πραγματικά
. Πραγματικά  δηλαδή το
δηλαδή το 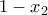 είναι η (μοναδική) ρίζα της
είναι η (μοναδική) ρίζα της 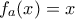 . Με άλλα λόγια
. Με άλλα λόγια  , όπως θέλαμε
, όπως θέλαμεΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες