Έχετε δίκιο, με συγχωρείτε, απο κεκτημένη ταχύτητα έκανα λάθος στο ρήμα "ανήκει" . Για την συμπάγεια ενός μετρικού χώρου μας δόθηκαν δύο ορισμοί:
1. Ένας μετρικός χώρος

λέγεται ακολουθιακά συμπαγής αν κάθε ακολουθία

στο

έχει υπακολουθία

που συγκλίνει σε κάποιο

.
Eπιπλέον αν

υποσύνολο του

λεμε οτι το Κ είναι ακολουθιακά συμπαγές αν για κάθε

στο K υπάρχει

2. Ένας μετρικός χώρος

λέγεται συμπαγής αν: Για κάθε ανοιχτή κάλυψη

του

μπορούμε να βρούμε πεπερασμένη υποκάλυψη
(δηλαδή υπάρχουν i_1, ... , i_N τέτοια ώστε
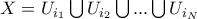
)
Ομοίως το

υποσύνολο του

λέγεται συμπαγές αν για κάθε οικογένεια

ανοιχτων συνόλων με
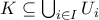
υπάρχουν πεπερασμένοι δείκτες

τέτοια ώστε

Σκέφτηκα φυσικά και τον τρόπο να δείξω οτι ειναι κλειστό και φραγμένο. Το φραγμένο φαίνεται απο τον ορισμό του συνόλου Κ. Μένει να δείξουμε οτι ειναι και κλειστό. Για να δείξω οτι ειναι κλειστό πρέπει να δείξω οτι κάθε ακολουθία μέσα στο Κ θα συγκλίνει μέσα στο Κ. Προφανώς δεν μπορώ να τις πάρω όλες, οπότε φαντάστηκα οτι θα χρειάζεται κάποιας μορφής με άτοπο. Αλλά δεν ήξερα πως να το δημιουργήσω το άτοπο.
Ετσι λοιπόν σκέφτηκα να χρησιμοποιήσω και τον 2ο ορισμό. Ο 2ος ορισμός όμως δεν μου λέει αν η οικογένεια ανοιχτών συνόλων

είναι υποσύνολο του

ή του

Στο ερώτημα 1) πράγματι, αφοπλίζει τελείως το επιχείρημά μου... έχω κολήσει !
Όσον αφορά τον αστερίσκο [*]
Το Κ μπορώ να το καλύψω με μία οικογένεια ανοιχτών μπαλών μέσα και έξω απο το Κ
λέγεται συμπαγές αν για κάθε οικογένεια ανοιχτών συνόλων

υπάρχουν πεπερασμένοι δείκτες
τέτοια ώστε
 . Ελπίζω να μην είναι απο δική μου έλλειψη.
. Ελπίζω να μην είναι απο δική μου έλλειψη. η οποία αποτελεί πεπερασμένη υποκάλυψη του Κ.
η οποία αποτελεί πεπερασμένη υποκάλυψη του Κ.
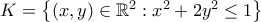

 η οποία αποτελεί πεπερασμένη υποκάλυψη του Κ.
η οποία αποτελεί πεπερασμένη υποκάλυψη του Κ. είναι συμπαγές, αν το
είναι συμπαγές, αν το 

 λέγεται ακολουθιακά συμπαγής αν κάθε ακολουθία
λέγεται ακολουθιακά συμπαγής αν κάθε ακολουθία  στο
στο  έχει υπακολουθία
έχει υπακολουθία  που συγκλίνει σε κάποιο
που συγκλίνει σε κάποιο  .
. 
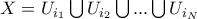 )
) στο
στο 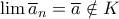 ...
... έξω απο το Κ.
έξω απο το Κ.  που έχει θετική απόσταση απο την έλλειψη. Και μέσα σε αυτήν την μπάλα υπάρχουν άπειροι όροι της
που έχει θετική απόσταση απο την έλλειψη. Και μέσα σε αυτήν την μπάλα υπάρχουν άπειροι όροι της  που ανήκουν στο Κ αλλά και παράλληλα στην μπάλα που είναι έξω απο το Κ και έτσι παίρνουμε το άτοπο ??
που ανήκουν στο Κ αλλά και παράλληλα στην μπάλα που είναι έξω απο το Κ και έτσι παίρνουμε το άτοπο ?? στοιχείων του
στοιχείων του 
 .
.
 τέτοιο ώστε
τέτοιο ώστε 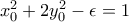

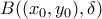 για την οποία ισχύει οτι
για την οποία ισχύει οτι 
 θα υπάρχουν άπειροι όροι της ακολουθίας
θα υπάρχουν άπειροι όροι της ακολουθίας  μέσα στην μπάλα.
μέσα στην μπάλα.
 ακολουθία πραγματικών με
ακολουθία πραγματικών με  και
και  για κάθε
για κάθε  , τότε και
, τότε και  . Σίγουρα το έχεις μάθει πολύ πριν κάνεις Μετρικούς Χώρους. Έχουμε λοιπόν
. Σίγουρα το έχεις μάθει πολύ πριν κάνεις Μετρικούς Χώρους. Έχουμε λοιπόν με
με  . Είναι τότε
. Είναι τότε  και
και  , οπότε
, οπότε  . Από
. Από  είναι
είναι  . Τελειώσαμε.
. Τελειώσαμε.