Θα ήθελα τη γνώμη σας για δύο σχετικά ερωτήματα:
(1) Αν υπάρχει μια απλή απόδειξη της ανισότητας
 για κάθε
για κάθε  , με το ίσον όταν
, με το ίσον όταν  , ΔΙΧΩΣ τη χρήση παραγώγων.
, ΔΙΧΩΣ τη χρήση παραγώγων. Έχω μία προσέγγιση αλλά έχει αρκετούς μετασχηματισμούς (οδηγεί στην
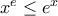 ).
).(2) Αν ζητούσαμε απλώς την εύρεση του ελαχίστου της παράστασης
 για κάθε
για κάθε  , θα ήταν εφικτή ΔΙΧΩΣ τη χρήση παραγώγων;
, θα ήταν εφικτή ΔΙΧΩΣ τη χρήση παραγώγων; Ευχαριστώ προκαταβολικά όποιον ασχοληθεί.

 , ισοδύναμα
, ισοδύναμα  , που ισχύει. Το τελευταίο βγαίνει βέβαια με παραγώγους αλλά μπορούμε και χωρίς, ανάλογα τι επιτρέπεται να χρησιμοποιήσουμε ως γνωστό. Π.χ. από Bernoulli έχουμε
, που ισχύει. Το τελευταίο βγαίνει βέβαια με παραγώγους αλλά μπορούμε και χωρίς, ανάλογα τι επιτρέπεται να χρησιμοποιήσουμε ως γνωστό. Π.χ. από Bernoulli έχουμε  .
.