Θ.Μ.Τ

Antonis Loutraris · #1

Καλησπέρα και καλή χρονιά!

Mία άσκηση που συνάντησα σήμερα:
Άς είναι μία 2 φορές παραγωγίσιμη συνάρτηση $f:\mathbb{R}\to\mathbb{R}$ για την οποία $\displaystyle{\lim_{x\to +\infty}f''(x)=0.}$
Δείξτε ότι κάθε $a\in\mathbb{R}$ , $\displaystyle{\lim_{x\to +\infty}\left(f(x+2a)-2f(x+a)+f(x)\right)=0.}$

Ενδεχομένως να δέχεται και σχολική λύση...

Λάμπρος Κατσάπας · #2

Antonis Loutraris έγραψε: ↑
Δευ Ιαν 14, 2019 12:08 am
Καλησπέρα και καλή χρονιά!

Mία άσκηση που συνάντησα σήμερα:
Άς είναι μία 2 φορές παραγωγίσιμη συνάρτηση $f:\mathbb{R}\to\mathbb{R}$ για την οποία $\displaystyle{\lim_{x\to +\infty}f''(x)=0.}$
Δείξτε ότι κάθε $a\in\mathbb{R}$ , $\displaystyle{\lim_{x\to +\infty}\left(f(x+2a)-2f(x+a)+f(x)\right)=0.}$

Ενδεχομένως να δέχεται και σχολική λύση...

Γεια σου Αντώνη και καλή χρονιά!

Η περίπτωση a=0

είναι τετριμμένη.

Για a>0

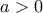με αλλαγή μεταβλητής αρκεί να δείξουμε ότι $\displaystyle{\lim_{x\to +\infty}\left(f(x+a)-2f(x)+f(x-a)\right)=0.}$

Από Taylor υπάρχουν $c \in(x,x+a),d \in(x-a,x)$ ώστε $\displaystyle f(x+a)=f(x)+{f}'(x)a+{f}''(c)\frac{a^2}{2}$ και $\displaystyle f(x-a)=f(x)-{f}'(x)a+{f}''(d)\frac{a^2}{2}$ .

Με πρόσθεση κατά μέλη $\displaystyle f(x+a)+f(x-a)-2f(x)=\left ( {f}''(c)+{f}''(d) \right )\frac{a^2}{2}\rightarrow 0$

Για a<0

κάνουμε πάλι τα ίδια.

#3

Antonis Loutraris έγραψε: ↑
Δευ Ιαν 14, 2019 12:08 am
Άς είναι μία 2 φορές παραγωγίσιμη συνάρτηση $f:\mathbb{R}\to\mathbb{R}$ για την οποία $\displaystyle{\lim_{x\to +\infty}f''(x)=0.}$
Δείξτε ότι κάθε $a\in\mathbb{R}$ , $\displaystyle{\lim_{x\to +\infty}\left(f(x+2a)-2f(x+a)+f(x)\right)=0.}$

Γεια σου Αντώνη.

Για το παραπάνω, με τρεις φορές ΘΜΤ υπάρχουν $\xi _1, \xi _2$ και μετά $\xi _3$ με $x+2a> \xi_1 > x+a > \xi_2 > x$ και $\xi_1 > \xi _3 > \xi_1$ τέτοια ώστε

$\displaystyle{| f(x+2a)-2f(x+a)+f(x)| =| \left ( f(x+2a)-f(x+a) \right ) - \left(f(x+a)-f(x)\right ) |= |f'(\xi_1)a- f'(\xi _2)a |=}$

$\displaystyle{= | f''(\xi _3) (\xi _1 - \xi_2)a| = | f''(\xi _3)| \cdot |\xi _1 - \xi_2 |\cdot |a|\le | f''(\xi _3)| \cdot |2a|\cdot |a|\to 0}$ (διότι $\xi_3> x \to \infty$ )

Θ.Μ.Τ

Θ.Μ.Τ

Re: Θ.Μ.Τ

Re: Θ.Μ.Τ

Μέλη σε σύνδεση