
με συνεχή δεύτερη παράγωγο και

Ορίζουμε την

με


Να δειχθεί ότι η
 είναι κυρτή.
είναι κυρτή.Συντονιστής: emouroukos





 είναι κυρτή.
είναι κυρτή. .Θεωρούμε την αλλαγή μεταβλητών
.Θεωρούμε την αλλαγή μεταβλητών ![u:[0,1]\rightarrow R,u(t )=t x,\forall t\in [0,1] u:[0,1]\rightarrow R,u(t )=t x,\forall t\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/412106b26be6df0f298f89f9a5a6e835.png) .Eίναι προφανές ότι η u είναι συνεχώς διαφορίσιμη στο πεδίο ορισμού της,με
.Eίναι προφανές ότι η u είναι συνεχώς διαφορίσιμη στο πεδίο ορισμού της,με ![u'(t)=x,\forall t \in [0,1],u(0)=0,u(1)=x u'(t)=x,\forall t \in [0,1],u(0)=0,u(1)=x](/forum/ext/geomar/texintegr/latexrender/pictures/e003ac1206a5e8fb4d34c938a8ff6d3b.png) και η f είναι συνεχής στο
και η f είναι συνεχής στο ![u([0,1])=[0,x] u([0,1])=[0,x]](/forum/ext/geomar/texintegr/latexrender/pictures/2fe4cfe616f53b1e300b4eb063510334.png) ,οπότε:
,οπότε: =
=
 είναι
είναι  ,ενώ επειδή
,ενώ επειδή  ,έπεται ότι
,έπεται ότι  .
.
 ,με
,με και
και ![\large \forall \varrho \in [0,1] \large \forall \varrho \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/6464e50da0f2d8e56e15b92364e12bf6.png)


Εφτιαξα την τελευταία σχέση ώστε να φαίνεται όπως πρέπει.perpendicular έγραψε: ↑Τρί Ιαν 08, 2019 8:25 amΚαλημέρα Σταύρο.
Έστω.Θεωρούμε την αλλαγή μεταβλητών
.Eίναι προφανές ότι η u είναι συνεχώς διαφορίσιμη στο πεδίο ορισμού της,με
και η f είναι συνεχής στο
,οπότε:
=
Μέχρι τώρα δείξαμε ότιείναι
,ενώ επειδή
,έπεται ότι
.
Άρα έχουμε ότι
Τελικά λόγω της (*) έχουμε ότι,με
και
ισχύει:
(όπου η ανισότητα προκύπτει από την κυρτότητα της f)
κι ως εκ τούτου η F είναι κυρτή
 σαν ολοκλήρωμα που περιέχει την
σαν ολοκλήρωμα που περιέχει την  .
.Η δεύτερη λύση γίνεται αποδεικνύοντας ότιΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Δευ Ιαν 07, 2019 7:18 pmΔίνεται η κυρτή συνάρτηση
με συνεχή δεύτερη παράγωγο και
Ορίζουμε την

με
Να δειχθεί ότι ηείναι κυρτή.

 του ΘΜΤ σε μια κυρτή συνάρτηση είναι αύξουσα και συνεχής συνάρτηση του χ
του ΘΜΤ σε μια κυρτή συνάρτηση είναι αύξουσα και συνεχής συνάρτηση του χ  Με
Με 
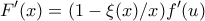
 λόγω του λήμματος άρα
λόγω του λήμματος άρα  αύξουσα συνάρτηση του χ και με τιμές θετικές αφού
αύξουσα συνάρτηση του χ και με τιμές θετικές αφού 
 αύξουσα αφού
αύξουσα αφού  κυρτή,
κυρτή,  αύξουσα από το λήμμα άρα η
αύξουσα από το λήμμα άρα η  αύξουσα
αύξουσα  αύξουσα δηλαδή
αύξουσα δηλαδή  κυρτή
κυρτήΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες