Γεια σου Σταύρο. Χάρηκα που τα είπαμε στην Αθήνα έστω και για ένα λεπτό. Ας ξεκινήσω με κάποια ερωτήματα. Τα άλλα θα τα παλέψω.
1. Κάνουμε ολοκλήρωση κατά παράγοντες, οπότε έχουμε:

και το ζητούμενο δείχθηκε.
2. Είναι

και αναγωγικά

,

. Τώρα , επαγωγικά έχουμε:

Παρομοίως, είναι

,

,

και επαγωγικά είναι:
 3.
3. Διαιρούμε τις δύο αυτές παραστάσεις και το αποτέλεσμα προκύπτει ... φυσικά.
4. Για

είναι
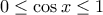
και

. Οπότε

. Τότε,

Οπότε από κριτήριο παρεμβολής είναι

. Συνδυάζοντας το αποτέλεσμα αυτό με το προηγούμενο ερώτημα έχουμε το ζητούμενο όριο.
5. Δύσκολο αποδείχθηκε αυτό. Έχουμε και λέμε ότι:

Εφόσον η
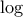
είναι αύξουσα τότε

Θέτω

. Τότε εύκολα βλέπουμε ότι
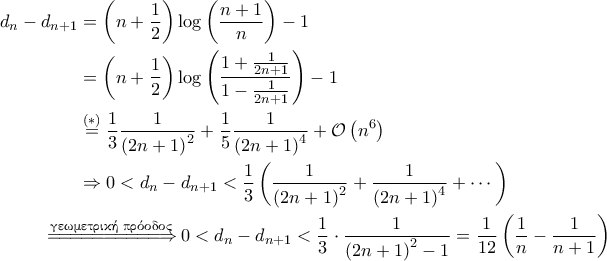

Αναπτύσουμε σε Taylor τη συνάρτηση
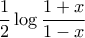
.
Από τα παραπάνω έχουμε ότι τόσο η ακολουθία
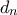
όσο και η

είναι αύξουσες. Συνεπώς ,

και μάλιστα
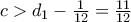
. Εκθετίζοντας τη
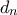
παίρνουμε το αποτέλεσμα.
6. Αποδείχθηκε πάνω.
Σταματώ εδώ μιας και έχω μάθημα και πρέπει να φύγω.



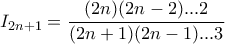






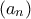 είναι μονότονη
είναι μονότονη 



 και αναγωγικά
και αναγωγικά  ,
,  . Τώρα , επαγωγικά έχουμε:
. Τώρα , επαγωγικά έχουμε:
 ,
,  ,
,  και επαγωγικά είναι:
και επαγωγικά είναι:
 είναι
είναι 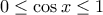 και
και  . Οπότε
. Οπότε  . Τότε,
. Τότε, 
 . Συνδυάζοντας το αποτέλεσμα αυτό με το προηγούμενο ερώτημα έχουμε το ζητούμενο όριο.
. Συνδυάζοντας το αποτέλεσμα αυτό με το προηγούμενο ερώτημα έχουμε το ζητούμενο όριο.
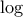 είναι αύξουσα τότε
είναι αύξουσα τότε 
 . Τότε εύκολα βλέπουμε ότι
. Τότε εύκολα βλέπουμε ότι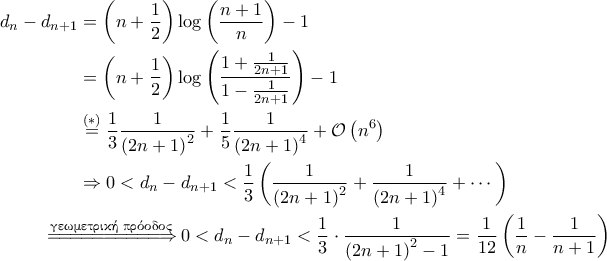
 Αναπτύσουμε σε Taylor τη συνάρτηση
Αναπτύσουμε σε Taylor τη συνάρτηση 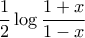 .
. 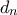 όσο και η
όσο και η  είναι αύξουσες. Συνεπώς ,
είναι αύξουσες. Συνεπώς ,
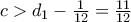 . Εκθετίζοντας τη
. Εκθετίζοντας τη 
 και
και  .
. ; Γιατί έτσι έχω και το πρώτο ερώτημα, με αυτή τη μορφή. Βέβαια όλα κλείνουν διότι:
; Γιατί έτσι έχω και το πρώτο ερώτημα, με αυτή τη μορφή. Βέβαια όλα κλείνουν διότι: