https://www.mathematica.gr/forum/viewto ... 53&t=62866
Εστω

με
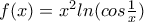
Να εξεταστεί αν υπάρχει το

Συντονιστής: emouroukos
Μη αναγνωσμένη δημοσίευση από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ » Πέμ Οκτ 25, 2018 8:31 pm

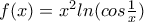

Μη αναγνωσμένη δημοσίευση από Demetres » Παρ Οκτ 26, 2018 2:20 pm
 .
. έχουμε
έχουμε  ,
, 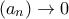 και
και  .
. , όπου
, όπου 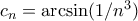 έχουμε
έχουμε  ,
,  . Επίσης
. Επίσης 
 .
.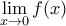 δεν υπάρχει. [Ούτε αν επιτρέψουμε να ισούται με
δεν υπάρχει. [Ούτε αν επιτρέψουμε να ισούται με  ή
ή  .]
.]Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες
Powered by phpBB® Forum Software © phpBB Limited
Style από Arty - Ενημέρωση phpBB 3.2 από MrGaby
Ελληνική μετάφραση από το phpbbgr.com
Το www.mathematica.gr δημιουργήθηκε από τους Γρηγόρη Κωστάκο και Αλέξανδρο Συγκελάκη
με τη βοήθεια των Στέλιου Μόσχογλου και Γιώργου Μαργαρίτη
GZIP: Off