
Να δειχθεί ότι

Συντονιστής: emouroukos
 , ἡ συνάρτηση
, ἡ συνάρτηση  εἶναι αὔξουσα στὰ διαστήματα
εἶναι αὔξουσα στὰ διαστήματα ![[2k\pi, (2k+1)\pi] [2k\pi, (2k+1)\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/5210af79aa7d94ff56400fb70fa93535.png) καὶ φθίνουσα στὰ
καὶ φθίνουσα στὰ ![[(2k+1)\pi, 2(k+1)\pi] [(2k+1)\pi, 2(k+1)\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/e7191d42399ae93936befe7ec18f52ad.png) , καὶ εὐκόλως διαπιστοῦται ὅτι λαμβάνει ἀπόλυτο μέγιστο γιὰ
, καὶ εὐκόλως διαπιστοῦται ὅτι λαμβάνει ἀπόλυτο μέγιστο γιὰ  , καὶ
, καὶ  .
.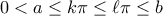 , Ἰσχύει ὅτι
, Ἰσχύει ὅτι
 , καὶ ἡ ἀκολουθία
, καὶ ἡ ἀκολουθία  εἶναι γνησίως φθίνουσα καὶ τείνει στὸ μηδέν.
εἶναι γνησίως φθίνουσα καὶ τείνει στὸ μηδέν. ![b\in [2m\pi, (2m+1)\pi] b\in [2m\pi, (2m+1)\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/5d26c399fad498324f4bc7894756fa15.png) , γιὰ κάποιο
, γιὰ κάποιο  , μὴ ἀρνητικὸ ἀκέραιο. Τότε ἡ τιμὴ τοῦ
, μὴ ἀρνητικὸ ἀκέραιο. Τότε ἡ τιμὴ τοῦ  , ἡ μεγιστοποιοῦσα τὴν
, ἡ μεγιστοποιοῦσα τὴν  εἶναι ἡ
εἶναι ἡ  , καὶ
, καὶ
![b\in [(2m+1)\pi, (2m+2)\pi] b\in [(2m+1)\pi, (2m+2)\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/19bd8eb297f8e274f415696c3e85b4a6.png) , γιὰ κάποιο
, γιὰ κάποιο  , μὴ ἀρνητικὸ ἀκέραιο. Τότε ἡ τιμὴ τοῦ
, μὴ ἀρνητικὸ ἀκέραιο. Τότε ἡ τιμὴ τοῦ  , ἡ μεγιστοποιοῦσα τὴν
, ἡ μεγιστοποιοῦσα τὴν 
 , ὁπότε
, ὁπότε  , εἴτε ἡ
, εἴτε ἡ  , ὁπότε, ὅπως κὰ στὴν Β-1, λαμβάνομε ὅτι
, ὁπότε, ὅπως κὰ στὴν Β-1, λαμβάνομε ὅτι





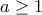 τότε
τότε 
 τότε
τότε 
 του
του  ενω το δεύτερο του
ενω το δεύτερο του  προκύπτει το ζητούμενο
προκύπτει το ζητούμενοΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες