viewtopic.php?f=59&t=52980
Εστω ακολουθία

με
 και
και 
1)Δείξτε ότι η σειρά

αποκλίνει
2)Δείξτε ότι η σειρά

για

συγκλίνει
Συντονιστής: emouroukos

 και
και 



Με άθροισμα Cauchy παίρνονταςΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιαν 09, 2018 9:58 pmΕστω ακολουθία
μεκαι
1)Δείξτε ότι η σειρά
αποκλίνει
 έχουμε
έχουμε 
Κάπου έχει απαντηθεί από το Δημήτρη. ( Demetres ) Πού; Απλά γράφω τη λύση του που είχα κρατήσει για το booklet με τις ασκήσεις στην Ανάλυση.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τρί Ιαν 09, 2018 9:58 pmΜε αφορμή λύσης του
viewtopic.php?f=59&t=52980
Εστω ακολουθία
μεκαι
1)Δείξτε ότι η σειρά
αποκλίνει.
 . Τότε:
. Τότε: Απόδειξη: Χρησιμοποιούμε επαγωγή στο
Απόδειξη: Χρησιμοποιούμε επαγωγή στο  . Για
. Για  είναι τετριμμένο. Έστω ότι ισχύει για
είναι τετριμμένο. Έστω ότι ισχύει για  τότε:
τότε: Οπότε ισχύει για
Οπότε ισχύει για  και το λήμμα απεδείχθει. Εφόσον
και το λήμμα απεδείχθει. Εφόσον 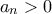 και
και  μπορούμε να βρούμε
μπορούμε να βρούμε  τέτοια ώστε
τέτοια ώστε  για κάθε
για κάθε  . Αλλά τότε:
. Αλλά τότε: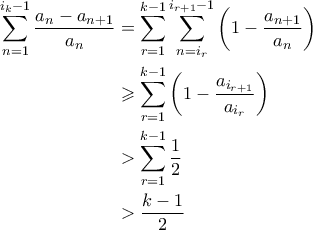 όπου στη πρώτη ανισότητα χρησιμοποιήσαμε το λήμμα.
όπου στη πρώτη ανισότητα χρησιμοποιήσαμε το λήμμα.

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες