Έτος Μαθηματικών 2018 - "Παιχνίδι" με την ανισότητα e^x>=x+1
Συντονιστής: emouroukos
Έτος Μαθηματικών 2018 - "Παιχνίδι" με την ανισότητα e^x>=x+1
Το 2018 ανακηρύχτηκε από το Υπουργείο Παιδείας ως «Έτος Μαθηματικών» λόγω της συμπλήρωσης των 100 χρόνων από την ίδρυση της ΕΜΕ. Πολλές σχετικές εκδηλώσεις και άλλες δραστηριότητες θα λάβουν χώρα κατά τη διάρκεια του 2018. Στα πλαίσια των δικών μας δραστηριοτήτων εκδίδουμε σήμερα, 2η μέρα του χρόνου, μια πρωτότυπη εργασία σχετικά με τη δημιουργική διδασκαλία της Ανάλυσης στο Λύκειο.
Κατεβάσετε την εργασία από εδώ...
http://www.pe03.gr/abc/ergasies/lyk-c-p ... ta-ex.html
Κατεβάσετε την εργασία από εδώ...
http://www.pe03.gr/abc/ergasies/lyk-c-p ... ta-ex.html
τελευταία επεξεργασία από spatharas σε Παρ Ιαν 05, 2018 9:42 am, έχει επεξεργασθεί 1 φορά συνολικά.
Λέξεις Κλειδιά:
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Έτος Μαθηματικών 2018 - "Παιχνίδι" με την ανισότητα e^x>=x+1
Ευχαριστώντας τον Δημήτρη Σπαθάρα για την εργασία που απευθύνεται στους μάχιμους συναδέλφους της τάξης και που την μοιράζεται με όλους εμάς , δηλώνω αρχικά ότι συμφωνώ κατά γράμμα με το εισαγωγικό κείμενο: "Προσανατολισμένα Μαθηματικά εναντίον Μαθηματικών Προσανατολισμού". Όλοι όσοι εμπλέκονται στην εκπαίδευση μαθητών, φαντάζομαι ότι, έχουν συναντήσει κάποιους μαθητές που ενώ έχουν αποκτήσει την ικανότητα να εντοπίζουν με μια ματιά το υπαρξιακό θεώρημα που κρύβει η στολισμένη σαν χριστουγεννιάτικο δέντρο παράσταση, εντούτοις μεσούσης της προετοιμασίας για τις Πανελλήνιες (μελλοντικά ΚΟΕΔ: Κεντρικά Οργανωμένες Εξεταστικές Διαδικασίες), αδυνατούν να χρησιμοποιήσουν σωστά τη συνεπαγωγή ή εκφράζουν απορίες του τύπου: "γιατί μετράμε πια τα τόξα σε ακτίνια κι όχι σε μοίρες όπως στο Γυμνάσιο κύριε;"
Μια πρόταση:
Στη σελίδα 9 τίθεται το ενδιαφέρον ερώτημα: Αν τέτοιος ώστε
τέτοιος ώστε  για κάθε
για κάθε  , τότε η μοναδική τιμή του
, τότε η μοναδική τιμή του  είναι
είναι 
Αρχικά (1ο βήμα) γίνεται διερεύνηση με τη χρήση λογιστικού φύλλου, διατυπώνεται η εικασία ότι η δεν παίρνει αρνητικές τιμές και ενισχύεται η εικασία ότι
δεν παίρνει αρνητικές τιμές και ενισχύεται η εικασία ότι  με την παρατήρηση των γραφικών παραστάσεων (2ο βήμα).
με την παρατήρηση των γραφικών παραστάσεων (2ο βήμα).
Κατόπιν (3ο βήμα) ζητείται η απόδειξη της συνεπαγωγής: Αν και
και  για κάθε
για κάθε  , τότε
, τότε  .
.
Η απόδειξη δίνεται με τη χρήση του Θεωρήματος Fermat και είναι ασφαλώς πλήρης.
Εδώ, όμως, θα πρότεινα στο 3ο βήμα να μην ζητηθεί η απόδειξη της συνεπαγωγής, αλλά να απαντηθεί το αρχικό ερώτημα ή κάνοντας το ακόμα πιο δύσκολο, να ζητηθεί η τιμή του .
.
Τότε η απόδειξη του 3ου βήματος θα απαιτούσε και την επαλήθευση της μοναδικότητας της ρίζας . Η οποία είναι σχεδόν άμεση: Βρίσκοντας ότι είναι θετικό το πρόσημο της 2ης παραγώγου, εξασφαλίζουμε ότι είναι γνησίως αύξουσα η πρώτη παράγωγος, άρα η προφανής ρίζα (από το Θ. Fermat)
. Η οποία είναι σχεδόν άμεση: Βρίσκοντας ότι είναι θετικό το πρόσημο της 2ης παραγώγου, εξασφαλίζουμε ότι είναι γνησίως αύξουσα η πρώτη παράγωγος, άρα η προφανής ρίζα (από το Θ. Fermat)  είναι μοναδική.
είναι μοναδική.
Τι κερδίζουμε έτσι: Διδάσκουμε μέσω του παραδείγματος την έννοια της απόδειξης και της διερεύνησης.
Στην πρώτη περίπτωση ζητάμε από τους μαθητές να αποδείξουν την αλήθεια μιας πρότασης που εμείς έχουμε εκ των προτέρων εξασφαλίσει, οπότε δεν χρειάζεται να διερευνήσουν αν η τιμή που βρήκαν είναι μοναδική. Τούς αρκεί ότι απέδειξαν αυτό που τους ζητάμε.
Στη δεύτερη, τους ζητάμε να διερευνήσουν τις δυνατές περιπτώσεις μιας μαθηματικές σχέσης.
Αξίζει, νομίζω να τονίσουμε τη διαφορά των δύο περιπτώσεων, που προκαλείται με μια φαινομενικά μικρή διαφορά στη διατύπωση.
ΣΧΟΛΙΑ:
(1) Για το φαινόμενο της αντικατάστασης των εκφωνήσεων παλαιού τύπου εξετάσεων: "Βρείτε, εξετάστε, λύστε, διερευνήστε" με τις εκφωνήσεις που περιείχαν ερωτήσεις σκαλοπάτια με μαξιλάρια, όπως π.χ.: "Αν ισχύει.... αποδείξτε ότι " κ.ο.κ. έχουν γραφτεί πολλά. Ο κύριος λόγος είναι η αναγκαιότητα αποσύνδεσης της βαθμολόγησης των επιμέρους ερωτημάτων στις πανελλήνιες. Δηλαδή αν κάποιος μαθητής αδυνατεί να υπολογίσει τις τιμές των
" κ.ο.κ. έχουν γραφτεί πολλά. Ο κύριος λόγος είναι η αναγκαιότητα αποσύνδεσης της βαθμολόγησης των επιμέρους ερωτημάτων στις πανελλήνιες. Δηλαδή αν κάποιος μαθητής αδυνατεί να υπολογίσει τις τιμές των  στο πρώτο ερώτημα να μην χάνει και τα υπόλοιπα.
στο πρώτο ερώτημα να μην χάνει και τα υπόλοιπα.
Τη τακτική αυτή που την έχουμε κάνει λάστιχο, αφού μέχρι και στο Γυμνάσιο βλέπουμε εκφωνήσεις του τύπου: "Αποδείξτε ότι τόσο συν τόσο κάνει τόσο", αντί για την "παλαιού τύπου" ερώτηση: "Βρείτε πόσο κάνει το τόσο συν το τόσο". Για τις παρενέργειες αυτής της τακτικής δείτε και στο σχετικό κεφάλαιο στο βιβλίο του Γ. Θωμαΐδη: "Μαθηματικά και εξετάσεις".
(2) Στα πρώτα χρόνια του είχε διεξαχθεί μια πολύ ενδιαφέρουσα συζήτηση (ΕΔΩ) με αφορμή το παρόμοιο θέμα των πανελληνίων του 2009.
είχε διεξαχθεί μια πολύ ενδιαφέρουσα συζήτηση (ΕΔΩ) με αφορμή το παρόμοιο θέμα των πανελληνίων του 2009.
Μια πρόταση:
Στη σελίδα 9 τίθεται το ενδιαφέρον ερώτημα: Αν
 τέτοιος ώστε
τέτοιος ώστε  για κάθε
για κάθε  , τότε η μοναδική τιμή του
, τότε η μοναδική τιμή του  είναι
είναι 
Αρχικά (1ο βήμα) γίνεται διερεύνηση με τη χρήση λογιστικού φύλλου, διατυπώνεται η εικασία ότι η
 δεν παίρνει αρνητικές τιμές και ενισχύεται η εικασία ότι
δεν παίρνει αρνητικές τιμές και ενισχύεται η εικασία ότι  με την παρατήρηση των γραφικών παραστάσεων (2ο βήμα).
με την παρατήρηση των γραφικών παραστάσεων (2ο βήμα).Κατόπιν (3ο βήμα) ζητείται η απόδειξη της συνεπαγωγής: Αν
 και
και  για κάθε
για κάθε  , τότε
, τότε  .
.Η απόδειξη δίνεται με τη χρήση του Θεωρήματος Fermat και είναι ασφαλώς πλήρης.
Εδώ, όμως, θα πρότεινα στο 3ο βήμα να μην ζητηθεί η απόδειξη της συνεπαγωγής, αλλά να απαντηθεί το αρχικό ερώτημα ή κάνοντας το ακόμα πιο δύσκολο, να ζητηθεί η τιμή του
 .
.Τότε η απόδειξη του 3ου βήματος θα απαιτούσε και την επαλήθευση της μοναδικότητας της ρίζας
 . Η οποία είναι σχεδόν άμεση: Βρίσκοντας ότι είναι θετικό το πρόσημο της 2ης παραγώγου, εξασφαλίζουμε ότι είναι γνησίως αύξουσα η πρώτη παράγωγος, άρα η προφανής ρίζα (από το Θ. Fermat)
. Η οποία είναι σχεδόν άμεση: Βρίσκοντας ότι είναι θετικό το πρόσημο της 2ης παραγώγου, εξασφαλίζουμε ότι είναι γνησίως αύξουσα η πρώτη παράγωγος, άρα η προφανής ρίζα (από το Θ. Fermat)  είναι μοναδική.
είναι μοναδική.Τι κερδίζουμε έτσι: Διδάσκουμε μέσω του παραδείγματος την έννοια της απόδειξης και της διερεύνησης.
Στην πρώτη περίπτωση ζητάμε από τους μαθητές να αποδείξουν την αλήθεια μιας πρότασης που εμείς έχουμε εκ των προτέρων εξασφαλίσει, οπότε δεν χρειάζεται να διερευνήσουν αν η τιμή που βρήκαν είναι μοναδική. Τούς αρκεί ότι απέδειξαν αυτό που τους ζητάμε.
Στη δεύτερη, τους ζητάμε να διερευνήσουν τις δυνατές περιπτώσεις μιας μαθηματικές σχέσης.
Αξίζει, νομίζω να τονίσουμε τη διαφορά των δύο περιπτώσεων, που προκαλείται με μια φαινομενικά μικρή διαφορά στη διατύπωση.
ΣΧΟΛΙΑ:
(1) Για το φαινόμενο της αντικατάστασης των εκφωνήσεων παλαιού τύπου εξετάσεων: "Βρείτε, εξετάστε, λύστε, διερευνήστε" με τις εκφωνήσεις που περιείχαν ερωτήσεις σκαλοπάτια με μαξιλάρια, όπως π.χ.: "Αν ισχύει.... αποδείξτε ότι
 " κ.ο.κ. έχουν γραφτεί πολλά. Ο κύριος λόγος είναι η αναγκαιότητα αποσύνδεσης της βαθμολόγησης των επιμέρους ερωτημάτων στις πανελλήνιες. Δηλαδή αν κάποιος μαθητής αδυνατεί να υπολογίσει τις τιμές των
" κ.ο.κ. έχουν γραφτεί πολλά. Ο κύριος λόγος είναι η αναγκαιότητα αποσύνδεσης της βαθμολόγησης των επιμέρους ερωτημάτων στις πανελλήνιες. Δηλαδή αν κάποιος μαθητής αδυνατεί να υπολογίσει τις τιμές των  στο πρώτο ερώτημα να μην χάνει και τα υπόλοιπα.
στο πρώτο ερώτημα να μην χάνει και τα υπόλοιπα.Τη τακτική αυτή που την έχουμε κάνει λάστιχο, αφού μέχρι και στο Γυμνάσιο βλέπουμε εκφωνήσεις του τύπου: "Αποδείξτε ότι τόσο συν τόσο κάνει τόσο", αντί για την "παλαιού τύπου" ερώτηση: "Βρείτε πόσο κάνει το τόσο συν το τόσο". Για τις παρενέργειες αυτής της τακτικής δείτε και στο σχετικό κεφάλαιο στο βιβλίο του Γ. Θωμαΐδη: "Μαθηματικά και εξετάσεις".
(2) Στα πρώτα χρόνια του
τελευταία επεξεργασία από Γιώργος Ρίζος σε Τετ Ιαν 03, 2018 8:01 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: Έτος Μαθηματικών 2018 - "Παιχνίδι" με την ανισότητα e^x>=x+1
Κύριε Ρίζο να σας ευχαριστήσω για το ότι μπήκατε στον κόπο να ασχοληθείτε σχολαστικά με την εργασία μου και για τις εύστοχες παρατηρήσεις σας. Είναι αλήθεια ότι κάτι δεν μου άρεσε και μένα στα τρία ερωτήματα του αφορούν το θεώρημα του Fermat. Ξέρεται, όμως, επειδή είχα το νου μου σε πάρα πολλές παραμέτρους της όλης εργασίας και ο χρόνος πίεζε διότι ήθελα να το κυκλοφορήσω την πρωτοχρονιά, μου διέφυγε. Γεγονός είναι ότι στη συγκεκριμένη περίπτωση δεν υπάρχει λόγος να δοθεί έτσι το 3ο βήμα. Δεν υπάρχουν στη συνέχεια άλλα ερωτήματα στα οποία ενδεχομένως να εγκλωβιστεί ο μαθητής. Έκανα λοιπόν μια προσπάθεια και το διατύπωσα διαφορετικά. Ρίξτε μια ματιά ξανά στο αρχείο.
Για το θέμα της περαιτέρω απόδειξης της μοναδικότητας έχω κάποιες επιφυλάξεις. Νομίζω ότι όπως είναι, είναι εντάξει και η μοναδικότητα είναι εξασφαλισμένη. Εξάλλου έτσι το παρουσιάζει και το βιβλίο λύσεων. Μονοτονία και 1-1 για μια συνάρτηση με μεταβλητή το x και συμπέρασμα για τη μοναδικότητα της ρίζας μιας εξίσωσης που αφορά την παράμετρο α; Παρόλα αυτά ένα αντιπαράδειγμα θα ήταν πειστικό.
Ευχαριστώ και πάλι και καλή χρονιά.
Για το θέμα της περαιτέρω απόδειξης της μοναδικότητας έχω κάποιες επιφυλάξεις. Νομίζω ότι όπως είναι, είναι εντάξει και η μοναδικότητα είναι εξασφαλισμένη. Εξάλλου έτσι το παρουσιάζει και το βιβλίο λύσεων. Μονοτονία και 1-1 για μια συνάρτηση με μεταβλητή το x και συμπέρασμα για τη μοναδικότητα της ρίζας μιας εξίσωσης που αφορά την παράμετρο α; Παρόλα αυτά ένα αντιπαράδειγμα θα ήταν πειστικό.
Ευχαριστώ και πάλι και καλή χρονιά.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15763
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Έτος Μαθηματικών 2018 - "Παιχνίδι" με την ανισότητα e^x>=x+1
Χάριν ποικιλίας ας δούμε άλλη μία απόδειξη της  , η οποία είναι πολλή απλή αλλά κάπως εκτός ύλης.
, η οποία είναι πολλή απλή αλλά κάπως εκτός ύλης.
Πρώτον κάνω ένα σχόλιο: Η αποδεικτέα έχει ενδιαφέρον μόνο για καθώς για
καθώς για  η ανισότητα είναι αυτόματη (το αριστερό μέλος είναι
η ανισότητα είναι αυτόματη (το αριστερό μέλος είναι 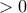 ενώ το δεξί
ενώ το δεξί  ). Αυτό θα μπορούσε να αξιοποιηθεί στην εργασία γιατί θα συντόμευε αρκετά σημεία. Στο παρακάτω θα κάνω χρήση της ανισότητα Bernoulli,
). Αυτό θα μπορούσε να αξιοποιηθεί στην εργασία γιατί θα συντόμευε αρκετά σημεία. Στο παρακάτω θα κάνω χρήση της ανισότητα Bernoulli,  για
για  , η οποία αποδεικνύεται με πολλούς τρόπους, π.χ. επαγωγικά.
, η οποία αποδεικνύεται με πολλούς τρόπους, π.χ. επαγωγικά.
Μένουμε λοιπόν στο . Είναι τότε
. Είναι τότε  . Παίρνοντας όριο
. Παίρνοντας όριο  προκύπτει
προκύπτει  , όπως θέλαμε.
, όπως θέλαμε.
 , η οποία είναι πολλή απλή αλλά κάπως εκτός ύλης.
, η οποία είναι πολλή απλή αλλά κάπως εκτός ύλης.Πρώτον κάνω ένα σχόλιο: Η αποδεικτέα έχει ενδιαφέρον μόνο για
 καθώς για
καθώς για  η ανισότητα είναι αυτόματη (το αριστερό μέλος είναι
η ανισότητα είναι αυτόματη (το αριστερό μέλος είναι 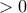 ενώ το δεξί
ενώ το δεξί  ). Αυτό θα μπορούσε να αξιοποιηθεί στην εργασία γιατί θα συντόμευε αρκετά σημεία. Στο παρακάτω θα κάνω χρήση της ανισότητα Bernoulli,
). Αυτό θα μπορούσε να αξιοποιηθεί στην εργασία γιατί θα συντόμευε αρκετά σημεία. Στο παρακάτω θα κάνω χρήση της ανισότητα Bernoulli,  για
για  , η οποία αποδεικνύεται με πολλούς τρόπους, π.χ. επαγωγικά.
, η οποία αποδεικνύεται με πολλούς τρόπους, π.χ. επαγωγικά. Μένουμε λοιπόν στο
 . Είναι τότε
. Είναι τότε  . Παίρνοντας όριο
. Παίρνοντας όριο  προκύπτει
προκύπτει  , όπως θέλαμε.
, όπως θέλαμε.- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5285
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Έτος Μαθηματικών 2018 - "Παιχνίδι" με την ανισότητα e^x>=x+1
Κύριε Σπαθάρα, ελπίζω να μην παρεξηγήθηκε η παρέμβασή μου ως απόπειρα κριτικής σε μια εργασία που την βρίσκω άκρως ενδιαφέρουσα, πλήρη στο θέμα της, διδακτική και εφαρμόσιμη ως ερευνητική δραστηριότητα σε μια ομάδα μαθητών (εννοείται με ενδιαφέρον για τα μαθηματικά).spatharas έγραψε: ↑Τετ Ιαν 03, 2018 2:29 pmΚύριε Ρίζο να σας ευχαριστήσω για το ότι μπήκατε στον κόπο να ασχοληθείτε σχολαστικά με την εργασία μου και για τις εύστοχες παρατηρήσεις σας. Είναι αλήθεια ότι κάτι δεν μου άρεσε και μένα στα τρία ερωτήματα του αφορούν το θεώρημα του Fermat. Ξέρεται, όμως, επειδή είχα το νου μου σε πάρα πολλές παραμέτρους της όλης εργασίας και ο χρόνος πίεζε διότι ήθελα να το κυκλοφορήσω την πρωτοχρονιά, μου διέφυγε. Γεγονός είναι ότι στη συγκεκριμένη περίπτωση δεν υπάρχει λόγος να δοθεί έτσι το 3ο βήμα. Δεν υπάρχουν στη συνέχεια άλλα ερωτήματα στα οποία ενδεχομένως να εγκλωβιστεί ο μαθητής. Έκανα λοιπόν μια προσπάθεια και το διατύπωσα διαφορετικά. Ρίξτε μια ματιά ξανά στο αρχείο.
Για το θέμα της περαιτέρω απόδειξης της μοναδικότητας έχω κάποιες επιφυλάξεις. Νομίζω ότι όπως είναι, είναι εντάξει και η μοναδικότητα είναι εξασφαλισμένη. Εξάλλου έτσι το παρουσιάζει και το βιβλίο λύσεων. Μονοτονία και 1-1 για μια συνάρτηση με μεταβλητή το x και συμπέρασμα για τη μοναδικότητα της ρίζας μιας εξίσωσης που αφορά την παράμετρο α; Παρόλα αυτά ένα αντιπαράδειγμα θα ήταν πειστικό.
Ευχαριστώ και πάλι και καλή χρονιά.
Η ανάρτηση μου είχε σκοπό να δώσει μια προέκταση και να επισημάνει τη διαφορετικότητα των εκφωνήσεων: "Αποδείξτε..." και "Βρείτε..."
Θα προσπαθήσω να περιγράψω με κάποια παραδείγματα τι εννοώ.
Αρχικά συμφωνούμε ότι η διατύπωση: "Αν
 και
και  (1) για κάθε
(1) για κάθε  , τότε
, τότε  " , ζητά την απόδειξη της συνεπαγωγής, οπότε δεν χρειάζεται επαλήθευση.
" , ζητά την απόδειξη της συνεπαγωγής, οπότε δεν χρειάζεται επαλήθευση.1ο παράδειγμα
Η εκφώνηση: "Αν
 και
και  (1) για κάθε
(1) για κάθε  , βρείτε το
, βρείτε το  " επίσης εξασφαλίζει στην εκφώνηση την ύπαρξη κάποιου
" επίσης εξασφαλίζει στην εκφώνηση την ύπαρξη κάποιου  που επαληθεύει την (1), οπότε, αφού η λύση (με την παραπάνω διαδικασία) οδηγεί σε μοναδική τιμή του
που επαληθεύει την (1), οπότε, αφού η λύση (με την παραπάνω διαδικασία) οδηγεί σε μοναδική τιμή του  , αυτή είναι η ζητούμενη.
, αυτή είναι η ζητούμενη.2ο παράδειγμα
Ας υποθέσουμε ότι εκ παραδρομής δινόταν το επόμενο ερώτημα ή κάποιο παρόμοιο (π.χ. 1η δέσμη 1997 κ.α.)
Αν
 και
και  (1) για κάθε
(1) για κάθε  , τότε
, τότε  .
."ΑΠΑΝΤΗΣΗ":
Έστω η συνάρτηση
 με τύπο
με τύπο  , με
, με  .
.Παρατηρούμε ότι
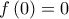 , οπότε
, οπότε 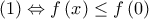 για κάθε
για κάθε  .
.Η
 είναι παραγωγίσιμη κι έχει ακρότατο για
είναι παραγωγίσιμη κι έχει ακρότατο για  , οπότε, από Θ. Fermat ισχύει
, οπότε, από Θ. Fermat ισχύει  και η απόδειξη ολοκληρώθηκε.
και η απόδειξη ολοκληρώθηκε. Παρατηρώ, όμως, ότι για
 είναι
είναι  , οπότε η τιμή
, οπότε η τιμή  δεν επαληθεύει την αρχική σχέση.
δεν επαληθεύει την αρχική σχέση. Παρουσιάζοντας τους παραπάνω συλλογισμούς στην τάξη πετυχαίνουμε ένα ενδιαφέρον "διδακτικό επεισόδιο", που απαιτεί την εξήγησή του.
Εδώ να σημειώσουμε ότι ουσιαστικά δεν έχουμε μαθηματικό λάθος, εφόσον από ψευδή υπόθεση έχουμε πάντα αληθή συνεπαγωγή, ότι τιμή αληθείας και να έχει το συμπέρασμα. Σαφώς αυτό ξεφεύγει από τα σχολικά πλαίσια, αλλά έχει τη μαθηματική αξία του ως θέμα.
3ο παράδειγμα
Ας αλλάξουμε φαινομενικά λίγο (στα μάτια των μαθητών), την εκφώνηση, ουσιαστικά όμως δίνουμε μια διαφορετική άσκηση:
Να προσδιοριστεί αν υπάρχει
 ώστε να είναι
ώστε να είναι  (1) για κάθε
(1) για κάθε  .
.Αν ακολουθούσαμε τα ίδια βήματα με τα παραπάνω παραδείγματα θα είχαμε:
Έστω η συνάρτηση
 με τύπο
με τύπο  , με
, με  .
.Παρατηρούμε ότι
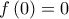 , οπότε
, οπότε 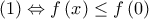 για κάθε
για κάθε  .
.Η
 είναι παραγωγίσιμη κι έχει ακρότατο για
είναι παραγωγίσιμη κι έχει ακρότατο για  , οπότε, από Θ. Fermat ισχύει
, οπότε, από Θ. Fermat ισχύει  .
.Εδώ, όμως, η εκφώνηση δεν εξασφαλίζει την ύπαρξη κάποιου
 που να ικανοποιεί την (1), οπότε χρειάζεται διερεύνηση.
που να ικανοποιεί την (1), οπότε χρειάζεται διερεύνηση.Είναι
 για κάθε
για κάθε  , άρα η
, άρα η  είναι γνησίως αύξουσα, οπότε είναι
είναι γνησίως αύξουσα, οπότε είναι  .
. Παρατηρώ, όμως, ότι για
 είναι
είναι  , οπότε η τιμή
, οπότε η τιμή  δεν επαληθεύει την αρχική σχέση, άρα δεν υπάρχει
δεν επαληθεύει την αρχική σχέση, άρα δεν υπάρχει  που να επαληθεύει την (1).
που να επαληθεύει την (1).Θα χαρώ πολύ να δω κι άλλες απόψεις στο θέμα αυτό και κυρίως σχετικά με την διδακτική ή μη αξία της ενασχόλησης στην τάξη ή σε ομάδες μαθητών με τέτοιου ύφους θέματα.
τελευταία επεξεργασία από Γιώργος Ρίζος σε Τετ Ιαν 03, 2018 11:10 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: Έτος Μαθηματικών 2018 - "Παιχνίδι" με την ανισότητα e^x>=x+1
Κύριε Λάμπρου
1) Στη σελίδα 13 και στην 3η ενδεικτική απάντηση διακρίνω τις περιπτώσεις x<=-1 και χ>-1. Στις άλλες αποδείξεις δεν έκρινα σκόπιμο να το αναφέρω γιατί δεν με διευκόλυνε σε κάτι.
2) Η απόδειξη που προτείνετε είναι άψογη αλλά κολλάμε στην ανισότητα Bernoulli που δεν είναι στη σχολική ύλη όπως και η επαγωγή. Έψαξα πολύ για μια απόδειξη με όρια και έκανα πολλές δοκιμές αλλά δεν κατέληξα σε κάτι παρουσιάσιμο. Ίσως αν μπορέσουμε να αποδείξουμε έμμεσα την ανισότητα Bernoulli με σχολικά μαθηματικά;
Ευχαριστώ πολύ, να είστε καλά.
1) Στη σελίδα 13 και στην 3η ενδεικτική απάντηση διακρίνω τις περιπτώσεις x<=-1 και χ>-1. Στις άλλες αποδείξεις δεν έκρινα σκόπιμο να το αναφέρω γιατί δεν με διευκόλυνε σε κάτι.
2) Η απόδειξη που προτείνετε είναι άψογη αλλά κολλάμε στην ανισότητα Bernoulli που δεν είναι στη σχολική ύλη όπως και η επαγωγή. Έψαξα πολύ για μια απόδειξη με όρια και έκανα πολλές δοκιμές αλλά δεν κατέληξα σε κάτι παρουσιάσιμο. Ίσως αν μπορέσουμε να αποδείξουμε έμμεσα την ανισότητα Bernoulli με σχολικά μαθηματικά;
Ευχαριστώ πολύ, να είστε καλά.
Re: Έτος Μαθηματικών 2018 - "Παιχνίδι" με την ανισότητα e^x>=x+1
Κύριε Λάμπρου
Τελικά κατάφερα μια απόδειξη με διάταξη ορίων η οποία να είναι παρουσιάσιμη. Έχω αλλάξει το αρχείο και είναι στη σελίδα 23. Σας παρακαλώ ρίξτε μια ματιά και πέστε μου τη γνώ μη σας.
Δ. Σπαθάρας
Τελικά κατάφερα μια απόδειξη με διάταξη ορίων η οποία να είναι παρουσιάσιμη. Έχω αλλάξει το αρχείο και είναι στη σελίδα 23. Σας παρακαλώ ρίξτε μια ματιά και πέστε μου τη γνώ μη σας.
Δ. Σπαθάρας
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15763
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Έτος Μαθηματικών 2018 - "Παιχνίδι" με την ανισότητα e^x>=x+1
Ευχαριστώ.
Θα το κοιτάξω με πρώτη ευκαιρία όταν μετά από λίγες μέρες βρεθώ σε υπολογιστή όπου η σύνδεση στο διαδίκτυο είναι κανονική και μπορέσω να κατεβάσω το αρχείο.
Μαντεύω ότι θα υπάρχει απόδειξη της
 (ή οι παραλλαγές της όπως
(ή οι παραλλαγές της όπως  ) για τα
) για τα  που μας ενδιαφέρουν, με χρήση παραγώγων. Αυτό γίνεται με πολλούς τρόπους όπως με χρήση του
που μας ενδιαφέρουν, με χρήση παραγώγων. Αυτό γίνεται με πολλούς τρόπους όπως με χρήση του 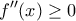 όπου
όπου  και λοιπά. Ανυπομονώ να το μελετήσω.
και λοιπά. Ανυπομονώ να το μελετήσω. Για την ώρα προσθέτω ότι βρήκα πολύ απλή απόδειξη της ανισότητας Bernoulli απολύτως μέσα στην Λυκειακή ύλη. Βλέπε το αμέσως από κάτω ποστ.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15763
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Έτος Μαθηματικών 2018 - "Παιχνίδι" με την ανισότητα e^x>=x+1
.
Τελικά η Bernoulli γίνεται με απλά μέσα, και θα μπορούσε να διδαχθεί στην Α' Λυκείου:
Θέλουμε να δείξουμε ότι
 για
για  . Ισοδύναμα
. Ισοδύναμα  για
για 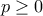 . Για
. Για 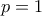 είναι προφανής. Για
είναι προφανής. Για  έχουμε
έχουμε 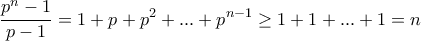 . Τελειώσαμε.
. Τελειώσαμε.Για
 κάνουμε ακριβώς το ίδιο αλλά με την ανισότητα αντεστραμμένη, εδώ
κάνουμε ακριβώς το ίδιο αλλά με την ανισότητα αντεστραμμένη, εδώ 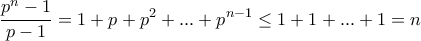 που πολλαπλασιάζοντας με την αρνητική ποσότητα
που πολλαπλασιάζοντας με την αρνητική ποσότητα  ξαναέρχεται στην μορφή που την θέλουμε.
ξαναέρχεται στην μορφή που την θέλουμε.Re: Έτος Μαθηματικών 2018 - "Παιχνίδι" με την ανισότητα e^x>=x+1
Κύριε Λάμπρου
Για το 1ο, σωστά το μαντέψατε. Όμως με χρήση μόνο 1ης παραγώγου αφού το πρόσημό της εύκολα μελετάται στοιχειωδώς.
Για το 2ο, η απόδειξη της ανισότητας Bernoulli είναι καταπληκτική. Δυστυχώς όμως τα διακριτά Μαθηματικά έχουν εξοβελιστεί από το σχολείο.
Σημείωση: Στην απόδειξη της ανισότητας (όπως είναι η παραλαγή που παρουσιάζετε) που έκανα με παραγώγους ως προς x, θεώρησα τον εκθέτη a να παίρνει τιμές στο διάστημα (1,+οο) και όχι διακριτές. Μετά τη διάταξη των ορίων υπολογίζω το όριο του πρώτου μέλους για a->+οο με De L Hospital αφού οι συνάρτηση ln(1+x/a) είναι παραγωγίσιμη ως προς a.
Δημ. Σπαθάρας
Σχολικός Σύμβουλος Μαθηματικών
Για το 1ο, σωστά το μαντέψατε. Όμως με χρήση μόνο 1ης παραγώγου αφού το πρόσημό της εύκολα μελετάται στοιχειωδώς.
Για το 2ο, η απόδειξη της ανισότητας Bernoulli είναι καταπληκτική. Δυστυχώς όμως τα διακριτά Μαθηματικά έχουν εξοβελιστεί από το σχολείο.
Σημείωση: Στην απόδειξη της ανισότητας (όπως είναι η παραλαγή που παρουσιάζετε) που έκανα με παραγώγους ως προς x, θεώρησα τον εκθέτη a να παίρνει τιμές στο διάστημα (1,+οο) και όχι διακριτές. Μετά τη διάταξη των ορίων υπολογίζω το όριο του πρώτου μέλους για a->+οο με De L Hospital αφού οι συνάρτηση ln(1+x/a) είναι παραγωγίσιμη ως προς a.
Δημ. Σπαθάρας
Σχολικός Σύμβουλος Μαθηματικών
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Έτος Μαθηματικών 2018 - "Παιχνίδι" με την ανισότητα e^x>=x+1


Αν
 περιττός τότε
περιττός τότε 
για

Αν
 άρτιος
άρτιος τότε
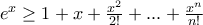
για

και

για

Re: Έτος Μαθηματικών 2018 - "Παιχνίδι" με την ανισότητα e^x>=x+1
Κύριε Παπαδόπουλε
Πολύ σωστά. Έτσι είναι, και σας ευχαριστώ.
Να όμως που ήθελα να το προσγειώσω σε μαθητικό επίπεδο; Δεν ήθελα ούτε σύμβολα καινούργια για το μαθητή να εισάγω (παραγοντικό) και χωρίς αυτά είναι δύσκολος ο χειρισμός. Περιορίστικα λοιπόν σε κάποιες ποιό απλές γενικεύσεις που εμφανίζονται σε σχολικά βοηθήματα. Θέλω έτσι να υπενθυμίσω στους συναδέλφους μου ότι πίσω από όλα αυτά κρύβεται (κατά μια εκδοχή) η σειρά Taylor. Ας δημιουργήσουν μόνοι τους όπου μπορούν και όπου είναι κατανοητοί. Μην ξεχνάμε ότι είμαι δημόσιος λειτουργός και δεν μπορώ να "πετάξω" παντού. Υπάρχει σχολική ύλη, υπάρχουν όρια. Μεταξύ μας συζητάμε ότι θέλετε. Η εργασία όμως απευθύνεται σε εκπαιδευτικούς που, ενδεχομένως να την εφαρμόσουν στην σχολική τάξη είτε ολόκληρη είτε μέρος της.
Ίσως σε μελλοντική έκδοση να κάνω χρήση της ιδέας σας για "μικρές" τιμές του n ώστε να φανεί καλύτερα η δημιουργία των ανισοτήτων και των συνόλων αναφοράς τους.
Καλή χρονιά.
Δ.Σ.
Πολύ σωστά. Έτσι είναι, και σας ευχαριστώ.
Να όμως που ήθελα να το προσγειώσω σε μαθητικό επίπεδο; Δεν ήθελα ούτε σύμβολα καινούργια για το μαθητή να εισάγω (παραγοντικό) και χωρίς αυτά είναι δύσκολος ο χειρισμός. Περιορίστικα λοιπόν σε κάποιες ποιό απλές γενικεύσεις που εμφανίζονται σε σχολικά βοηθήματα. Θέλω έτσι να υπενθυμίσω στους συναδέλφους μου ότι πίσω από όλα αυτά κρύβεται (κατά μια εκδοχή) η σειρά Taylor. Ας δημιουργήσουν μόνοι τους όπου μπορούν και όπου είναι κατανοητοί. Μην ξεχνάμε ότι είμαι δημόσιος λειτουργός και δεν μπορώ να "πετάξω" παντού. Υπάρχει σχολική ύλη, υπάρχουν όρια. Μεταξύ μας συζητάμε ότι θέλετε. Η εργασία όμως απευθύνεται σε εκπαιδευτικούς που, ενδεχομένως να την εφαρμόσουν στην σχολική τάξη είτε ολόκληρη είτε μέρος της.
Ίσως σε μελλοντική έκδοση να κάνω χρήση της ιδέας σας για "μικρές" τιμές του n ώστε να φανεί καλύτερα η δημιουργία των ανισοτήτων και των συνόλων αναφοράς τους.
Καλή χρονιά.
Δ.Σ.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες
