
με την ιδιότητα
Για
 ισχύει
ισχύει 
Θέτουμε

(
 είναι η
είναι η  παράγωγος)
παράγωγος)Να δειχθεί ότι για

ισχύει

Συντονιστής: emouroukos

 ισχύει
ισχύει 

 είναι η
είναι η  παράγωγος)
παράγωγος)

 . Οπότε
. Οπότε  για κάθε
για κάθε  .
.  είναι φθίνουσα. Επειδή
είναι φθίνουσα. Επειδή  πρέπει
πρέπει  για κάθε
για κάθε  . Επίσης πρέπει
. Επίσης πρέπει  για κάθε
για κάθε  αφού αν π.χ.
αφού αν π.χ.  για κάποιο
για κάποιο  , τότε θα είχαμε
, τότε θα είχαμε  για κάθε
για κάθε  . Αυτό δίνει
. Αυτό δίνει  για κάθε
για κάθε  . Όμως το
. Όμως το  είναι πολυώνυμο βαθμού
είναι πολυώνυμο βαθμού  , άτοπο.
, άτοπο. για κάθε
για κάθε  .
. αντί του ζητούμενου
αντί του ζητούμενου  .
.  ως πολυώνυμο άρτιου βαθμού έχει ολικό ελάχιστο, έστω στο
ως πολυώνυμο άρτιου βαθμού έχει ολικό ελάχιστο, έστω στο  , οπότε
, οπότε  . Άρα για κάθε
. Άρα για κάθε  έχουμε
έχουμε  , όπως "θέλαμε".
, όπως "θέλαμε".Μπορούμε να το τελειώσουμε πιο γρήγορα.
 είναι πολυώνυμο αρτίου βαθμού.
είναι πολυώνυμο αρτίου βαθμού. είναι γνησίως φθίνουσα μιας και το
είναι γνησίως φθίνουσα μιας και το  μηδενίζεται σε πεπερασμένο
μηδενίζεται σε πεπερασμένο 
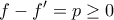 άρα
άρα  άρα
άρα  'αρα
'αρα  άρα
άρα  αμεσα το ζητούμενο
αμεσα το ζητούμενο αν το
αν το  έχει ρίζα τότε ακολουθούμε τον τρόπο του Μιχάλη η του Δημήτρη
έχει ρίζα τότε ακολουθούμε τον τρόπο του Μιχάλη η του ΔημήτρηΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 14 επισκέπτες