 και
και  . Από που λοιπόν προκύπτει ότι η
. Από που λοιπόν προκύπτει ότι η  είναι γνήσια αύξουσα;
είναι γνήσια αύξουσα;Αν μία συνάρτηση
 είναι συνεχής και
είναι συνεχής και  σε ένα διάστημα
σε ένα διάστημα  τότε είναι και γνησίως μονότονη στο
τότε είναι και γνησίως μονότονη στο  .
.Έστω
 με
με  . Αφού η
. Αφού η  είναι
είναι  ισχύει ότι
ισχύει ότι  . Ας υποθέσουμε ότι
. Ας υποθέσουμε ότι  και
και  . Θα δείξουμε ότι για κάθε
. Θα δείξουμε ότι για κάθε  ισχύει
ισχύει  .
.Θα εργασθούμε με την εις άτοπο απαγωγή. Έστω δηλαδή
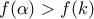 . Επειδή η
. Επειδή η  στο διάστημα
στο διάστημα ![[k,\beta] [k,\beta]](/forum/ext/geomar/texintegr/latexrender/pictures/06e2a96b9e7903c4bb20e3a16f2cb32d.png) είναι συνεχής, έχουμε σαν αποτέλεσμα να παίρνει όλες τις τιμές μεταξύ του
είναι συνεχής, έχουμε σαν αποτέλεσμα να παίρνει όλες τις τιμές μεταξύ του  και του
και του  . Άρα αφού
. Άρα αφού 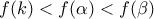 , υπάρχει
, υπάρχει  έτσι ώστε
έτσι ώστε  που είναι άτοπο διότι η
που είναι άτοπο διότι η  είναι
είναι 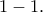
Ας υποθέσουμε τώρα ότι
 . Επειδή η
. Επειδή η  στο διάστημα
στο διάστημα ![[\alpha,k] [\alpha,k]](/forum/ext/geomar/texintegr/latexrender/pictures/1cf24d655fa84575b90b38b0f1f3a9dd.png) είναι συνεχής, έχουμε σαν αποτέλεσμα να παίρνει όλες τις τιμές μεταξύ του
είναι συνεχής, έχουμε σαν αποτέλεσμα να παίρνει όλες τις τιμές μεταξύ του  και του
και του  . Άρα αφού
. Άρα αφού  , υπάρχει
, υπάρχει  έτσι ώστε
έτσι ώστε  που είναι άτοπο διότι η
που είναι άτοπο διότι η  είναι
είναι  . Επίσης ισχύει ότι
. Επίσης ισχύει ότι  διότι η
διότι η  είναι
είναι 
Άρα ισχύει ότι
 για κάθε
για κάθε  δηλαδή η
δηλαδή η  είναι γνησίως αύξουσα στο τυχαίο
είναι γνησίως αύξουσα στο τυχαίο ![[\alpha,\beta] [\alpha,\beta]](/forum/ext/geomar/texintegr/latexrender/pictures/76ec9b92b11ea1475095ec6a47fccd53.png) υποσύνολο του
υποσύνολο του  . Με αντίστοιχο τρόπο αποδεικνύεται ότι η
. Με αντίστοιχο τρόπο αποδεικνύεται ότι η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  .
.
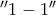 τον καθιστά τελικά σωστό, είναι άλλο πράγμα και πρέπει να αποδειχθεί .Δεν μπορεί όμως να αποτελεί πρόταση για τη λύση άσκησης ειδικά σε σχολικό επίπεδο.Μονοτονία χωρίς σύγκριση τυχαίων τιμών του διαστήματος
τον καθιστά τελικά σωστό, είναι άλλο πράγμα και πρέπει να αποδειχθεί .Δεν μπορεί όμως να αποτελεί πρόταση για τη λύση άσκησης ειδικά σε σχολικό επίπεδο.Μονοτονία χωρίς σύγκριση τυχαίων τιμών του διαστήματος ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) σε αυτό το επίπεδο της ύλης (ή με άτοπο κλπ) δεν μπορεί να προκύψει.
σε αυτό το επίπεδο της ύλης (ή με άτοπο κλπ) δεν μπορεί να προκύψει.
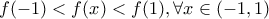 αλλά δεν είναι μονότονη. Αρκεί ένα πρόχειρο διάγραμμα, αλλά και το γεγονός ότι στο αντίστοιχο ανοικτό διάστημα η συνάρτηση είναι άρτια είναι αρκετό για να χαλάσει τη μονοτονία.
αλλά δεν είναι μονότονη. Αρκεί ένα πρόχειρο διάγραμμα, αλλά και το γεγονός ότι στο αντίστοιχο ανοικτό διάστημα η συνάρτηση είναι άρτια είναι αρκετό για να χαλάσει τη μονοτονία. , γι αυτό και την ανέβασα για συζήτηση. Αλλά η τυχαία επιλογή των
, γι αυτό και την ανέβασα για συζήτηση. Αλλά η τυχαία επιλογή των  αποδεικνύει ότι είναι γνήσια μονότονη στο
αποδεικνύει ότι είναι γνήσια μονότονη στο  με
με  και
και  είναι
είναι 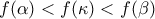
 , τότε η συνάρτηση
, τότε η συνάρτηση  με
με  είναι
είναι 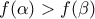 ; Θα πούμε τότε ότι η συνάρτηση είναι γνησίως φθίνουσα στο διάστημα αυτό και άρα γνησίως φθίνουσα στο διάστημα
; Θα πούμε τότε ότι η συνάρτηση είναι γνησίως φθίνουσα στο διάστημα αυτό και άρα γνησίως φθίνουσα στο διάστημα 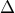 ;
; ![\left[ \alpha ,\beta \right] \left[ \alpha ,\beta \right]](/forum/ext/geomar/texintegr/latexrender/pictures/df943484c7129436c3cbc1d775a952e2.png) κάποια
κάποια  ώστε
ώστε 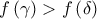 ;
;  γνωρίζουμε την διάταξη των
γνωρίζουμε την διάταξη των 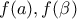 τότε έχουμε υποθέσει την μονοτονία της συνάρτησης οπότε τι θέλουμε να αποδείξουμε;
τότε έχουμε υποθέσει την μονοτονία της συνάρτησης οπότε τι θέλουμε να αποδείξουμε; η διάταξη των τιμών
η διάταξη των τιμών 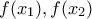 είναι η ίδια με την διάταξη των
είναι η ίδια με την διάταξη των 

![[\alpha ,\beta ] [\alpha ,\beta ]](/forum/ext/geomar/texintegr/latexrender/pictures/13ac621dab037fd260a54755bb2382a3.png) και τελικά γνησίως αύξουσα στο διάστημα
και τελικά γνησίως αύξουσα στο διάστημα  στο διάστημα
στο διάστημα  άρα λες
άρα λες  και προκύπτει αντίφαση γιατί είναι 1-1 . Είναι 1-1 στο
και προκύπτει αντίφαση γιατί είναι 1-1 . Είναι 1-1 στο  με
με  και ας υποθέσουμε λόγω του 1-1 ότι
και ας υποθέσουμε λόγω του 1-1 ότι 
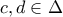 τυχόντα με
τυχόντα με  Θα δείξουμε ότι
Θα δείξουμε ότι 
 και
και  με
με ![t\in [0,1]. t\in [0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/de4ef1e33d30a0fa6fc661f8fed20bde.png)
![t\in [0,1] t\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d9a06fde4663cdd5b1ba693e9127232f.png) έχουμε ότι
έχουμε ότι 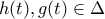 και επιπλέον
και επιπλέον 
 είναι συνεχής (σύνθεση και διαφορά συνεχών) και δεν μηδενίζεται λόγω τους 1-1 της
είναι συνεχής (σύνθεση και διαφορά συνεχών) και δεν μηδενίζεται λόγω τους 1-1 της  για κάθε
για κάθε ![[0,1]. [0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/5477054a4f15a08ccb4fce88af75dcb7.png)
 Οπότε πρέπει και
Οπότε πρέπει και 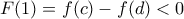 και έχουμε το ζητούμενο.
και έχουμε το ζητούμενο.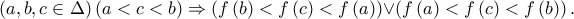

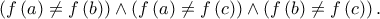
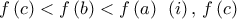


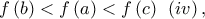

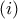 τότε από το θεώρημα ενδιάμεσων τιμών έχουμε την ύπαρξη εσωτερικού σημείου
τότε από το θεώρημα ενδιάμεσων τιμών έχουμε την ύπαρξη εσωτερικού σημείου  του διαστήματος
του διαστήματος  με την ιδιότητα
με την ιδιότητα  καθότι η
καθότι η  Αυτό όμως είναι άτοπο καθότι
Αυτό όμως είναι άτοπο καθότι  και
και  Κατά τον ίδιο τρόπο αποκλείονται οι περιπτώσεις
Κατά τον ίδιο τρόπο αποκλείονται οι περιπτώσεις 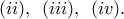 Αποδεικνύεται εύκολα ότι οι περιπτώσεις
Αποδεικνύεται εύκολα ότι οι περιπτώσεις  δεν ισχύουν ταυτόχρονα. Έτσι ισχύει η ιδιότητα
δεν ισχύουν ταυτόχρονα. Έτσι ισχύει η ιδιότητα  οπότε η συνάρτηση μας θα είναι γνήσια αύξουσα ή η ιδιότητα
οπότε η συνάρτηση μας θα είναι γνήσια αύξουσα ή η ιδιότητα  οπότε η συνάρτηση μας θα είναι γνήσια φθίνουσα. Αυτά όταν
οπότε η συνάρτηση μας θα είναι γνήσια φθίνουσα. Αυτά όταν ![\Delta =[a,b]. \Delta =[a,b].](/forum/ext/geomar/texintegr/latexrender/pictures/5830f7b911e9f11e4a93700f5df15da6.png)
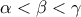 το να αποκλειστούν όλες οι άλλες περιπτώσεις εκτός από την
το να αποκλειστούν όλες οι άλλες περιπτώσεις εκτός από την  και την
και την  και υπόθεση ότι έστω δεν είναι γνήσια μονότονη δεν έχουμε φτάσει σε άτοπο. Σε κλειστο διάστημα είναι οκ η απόδειξη. κ. Lourida ακριβώς αυτή την απόδειξη εννοούσα προβληματική και με βασανίζει ο ερώτημα. Αποδείχθηκε για όλες τις τριάδες ότι θα ισχύει ή το ένα ή το άλλο; Μάλλον όχι. Μένει να ελέγξουμε την απόδειξη του ημι-συνώνυμου smar. Με προβληματίζει που στην βιβλιογραφία, με την ως τώρα έρευνα μου, η πρόταση υπάρχει μόνο για κλειστό διάστημα.
και υπόθεση ότι έστω δεν είναι γνήσια μονότονη δεν έχουμε φτάσει σε άτοπο. Σε κλειστο διάστημα είναι οκ η απόδειξη. κ. Lourida ακριβώς αυτή την απόδειξη εννοούσα προβληματική και με βασανίζει ο ερώτημα. Αποδείχθηκε για όλες τις τριάδες ότι θα ισχύει ή το ένα ή το άλλο; Μάλλον όχι. Μένει να ελέγξουμε την απόδειξη του ημι-συνώνυμου smar. Με προβληματίζει που στην βιβλιογραφία, με την ως τώρα έρευνα μου, η πρόταση υπάρχει μόνο για κλειστό διάστημα. για να είναι η συνάρτηση γνήσια μονότονη.
για να είναι η συνάρτηση γνήσια μονότονη.
 είναι οι παραμετρικοποιήσεις των ευθυγράμμων τμημάτων από το
είναι οι παραμετρικοποιήσεις των ευθυγράμμων τμημάτων από το  στο
στο  και από το
και από το  στο
στο 