 για την οποία ισχύει
για την οποία ισχύει  και
και 
Να αποδείξετε ότι η
 έχει μία πιθανή θέση σημείου καμπής.
έχει μία πιθανή θέση σημείου καμπής. Μπορούμε να δείξουμε ότι υπάρχει υποχρεωτικά θέση σημείου καμπής;
Συντονιστής: emouroukos
 για την οποία ισχύει
για την οποία ισχύει  και
και 
 έχει μία πιθανή θέση σημείου καμπής.
έχει μία πιθανή θέση σημείου καμπής. Ισχύει
 , άρα υπάρχει πιθανό σημείο καμπής.
, άρα υπάρχει πιθανό σημείο καμπής. για κάθε
για κάθε  .
. είναι θέση ολικού μεγίστου, οπότε από Fermat ισχύει
είναι θέση ολικού μεγίστου, οπότε από Fermat ισχύει  .
.Δεν έχουμε πληροφορίες για τις τιμές της
 αριστερά του μηδενός, οπότε το παραπάνω συμπέρασμα δεν ισχύει -- προφανές αντιπαράδειγμα η
αριστερά του μηδενός, οπότε το παραπάνω συμπέρασμα δεν ισχύει -- προφανές αντιπαράδειγμα η  (κατάλληλα τροποποιημένη για μεγάλα θετικά
(κατάλληλα τροποποιημένη για μεγάλα θετικά  ).
). και
και  , οπότε
, οπότε  λόγω των
λόγω των 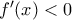 και
και  .
.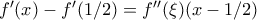 στην περίπτωση που υπάρχει
στην περίπτωση που υπάρχει 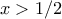 [
[ ]τέτοιο ώστε
]τέτοιο ώστε  [
[ ], στην αντίθετη περίπτωση η
], στην αντίθετη περίπτωση η  δίνει
δίνει  , άτοπο.
, άτοπο. και συνεχείας της
και συνεχείας της  ... συμπεραίνουμε ότι υπάρχει ένα τουλάχιστον σημείο μηδενισμού της
... συμπεραίνουμε ότι υπάρχει ένα τουλάχιστον σημείο μηδενισμού της  .
. σημείο καμπής της
σημείο καμπής της  ; Τα σημεία αρνητικότητας της
; Τα σημεία αρνητικότητας της  και τα σημεία θετικότητας της
και τα σημεία θετικότητας της  είναι ανοικτά σύνολα (λόγω συνεχείας της
είναι ανοικτά σύνολα (λόγω συνεχείας της  ), άρα ενώσεις αριθμησίμου το πολύ σε πλήθος ανοικτών διαστημάτων. Σκέφτομαι ότι θα μπορούσαμε να έχουμε αριθμησίμου πλήθους διαστήματα αρνητικότητας με μήκη τείνοντα στο μηδέν μέχρι κάποιο σημείο
), άρα ενώσεις αριθμησίμου το πολύ σε πλήθος ανοικτών διαστημάτων. Σκέφτομαι ότι θα μπορούσαμε να έχουμε αριθμησίμου πλήθους διαστήματα αρνητικότητας με μήκη τείνοντα στο μηδέν μέχρι κάποιο σημείο  και από εκεί και πέρα, ανάποδα, αριθμησίμου πλήθους διαστήματα θετικότητας με αυξανόμενα μήκη: το
και από εκεί και πέρα, ανάποδα, αριθμησίμου πλήθους διαστήματα θετικότητας με αυξανόμενα μήκη: το  ΔΕΝ θα ήταν σημείο καμπής καθώς θα είχαμε άπειρα σημεία μηδενισμού της
ΔΕΝ θα ήταν σημείο καμπής καθώς θα είχαμε άπειρα σημεία μηδενισμού της  εκατέρωθεν του -- αυτά τα σημεία μηδενισμού θα 'διαχώριζαν' τα διαστήματα αρνητικότητας μεταξύ τους (το κάθε διάστημα από το επόμενο του) και, αναλόγως, θα 'διαχώριζαν' τα διαστήματα θετικότητας μεταξύ τους.
εκατέρωθεν του -- αυτά τα σημεία μηδενισμού θα 'διαχώριζαν' τα διαστήματα αρνητικότητας μεταξύ τους (το κάθε διάστημα από το επόμενο του) και, αναλόγως, θα 'διαχώριζαν' τα διαστήματα θετικότητας μεταξύ τους. , ευθεία αρνητικής κλίσης στο
, ευθεία αρνητικής κλίσης στο ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) , και κυρτή στο
, και κυρτή στο  . [Η ύπαρξη και κατασκευή μιας τέτοιας συνάρτησης -- με 'διάστημα καμπής' αντί σημείου καμπής -- φαίνεται απλή, αν όμως τεθεί θέμα ύπαρξης τρίτης παραγώγου (ή ύπαρξης όλων των παραγώγων) -- τότε τα πράγματα αλλάζουν! (Θα επαναφέρω μετά τις διακοπές αν δεν υπάρξουν πληρέστερες απαντήσεις...)]
. [Η ύπαρξη και κατασκευή μιας τέτοιας συνάρτησης -- με 'διάστημα καμπής' αντί σημείου καμπής -- φαίνεται απλή, αν όμως τεθεί θέμα ύπαρξης τρίτης παραγώγου (ή ύπαρξης όλων των παραγώγων) -- τότε τα πράγματα αλλάζουν! (Θα επαναφέρω μετά τις διακοπές αν δεν υπάρξουν πληρέστερες απαντήσεις...)]Κάτι δεν κατάλαβες καλά.
 , υποχρεωτικά θα έχουμε ότι
, υποχρεωτικά θα έχουμε ότι  για κάθε
για κάθε  στο
στο  , λόγω μονοτονίας και συνέχεια της πρώτη παραγώγου(αν υπήρχε
, λόγω μονοτονίας και συνέχεια της πρώτη παραγώγου(αν υπήρχε  ώστε
ώστε 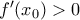 , τότε λόγω συνέχειας της παραγώγου η παράγωγος θα ήταν θετική κοντά στο
, τότε λόγω συνέχειας της παραγώγου η παράγωγος θα ήταν θετική κοντά στο  , άρα και γνησίως αύξουσα εκεί το οποίο είναι άτοπο.)
, άρα και γνησίως αύξουσα εκεί το οποίο είναι άτοπο.)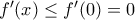 για κάθε
για κάθε  πραγματικό.
πραγματικό. , το οποίο σημαίνει ότι
, το οποίο σημαίνει ότι  , από Fermat.
, από Fermat.ΌΝΤΩΣ, το "φθίνουσα στοstranger έγραψε: ↑Παρ Αύγ 05, 2022 7:40 pmΚάτι δεν κατάλαβες καλά.
Αφού η συνάρτηση είναι γνησίως φθίνουσα στο, υποχρεωτικά θα έχουμε ότι
για κάθε
στο
, λόγω μονοτονίας και συνέχεια της πρώτη παραγώγου(αν υπήρχε
ώστε
, τότε λόγω συνέχειας της παραγώγου η παράγωγος θα ήταν θετική κοντά στο
, άρα και γνησίως αύξουσα εκεί το οποίο είναι άτοπο.)
Άρα έχουμεγια κάθε
πραγματικό.
Άρα η παράγωγος έχει ολικό μέγιστο στο, το οποίο σημαίνει ότι
, από Fermat.
 " το διάβασα ως "φθίνουσα στο
" το διάβασα ως "φθίνουσα στο 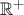 " .... και κάτι μου λέει ότι αυτό εννοούσε ο Θανάσης, καθώς αυτό καθιστά το πρόβλημα ενδιαφέρον!
" .... και κάτι μου λέει ότι αυτό εννοούσε ο Θανάσης, καθώς αυτό καθιστά το πρόβλημα ενδιαφέρον!Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες