 , να κατασκευαστεί (με κανόνα και διαβήτη) η εφαπτόμενη της
, να κατασκευαστεί (με κανόνα και διαβήτη) η εφαπτόμενη της  σε τυχαίο σημείο της , στις παρακάτω περιπτώσεις:
σε τυχαίο σημείο της , στις παρακάτω περιπτώσεις:Α ΟΜΑΔΑ:
α)
 , β)
, β) , γ)
, γ)
Β ΟΜΑΔΑ:
α)
 , β)
, β) , γ)
, γ)
Γ ΟΜΑΔΑ:
α)
 , β)
, β)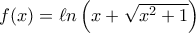 , γ)
, γ)
Συντονιστής: emouroukos
 , να κατασκευαστεί (με κανόνα και διαβήτη) η εφαπτόμενη της
, να κατασκευαστεί (με κανόνα και διαβήτη) η εφαπτόμενη της  σε τυχαίο σημείο της , στις παρακάτω περιπτώσεις:
σε τυχαίο σημείο της , στις παρακάτω περιπτώσεις: , β)
, β) , γ)
, γ)
 , β)
, β) , γ)
, γ)
 , β)
, β)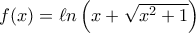 , γ)
, γ)
 , παραγωγίσιμη στο
, παραγωγίσιμη στο  και σημείο της
και σημείο της  και θέλουμε την κατασκευή της εφαπτομένης της στο σημείο αυτό μία γενική αντιμετώπιση είναι η εξής:
και θέλουμε την κατασκευή της εφαπτομένης της στο σημείο αυτό μία γενική αντιμετώπιση είναι η εξής: διάφορο του
διάφορο του  . Βρίσκουμε στην συνέχεια την εξίσωση της κάθετης ευθείας στην εφαπτομένη και στο σημείο
. Βρίσκουμε στην συνέχεια την εξίσωση της κάθετης ευθείας στην εφαπτομένη και στο σημείο  και προσδιορίζουμε ένα σημείο της, έστω
και προσδιορίζουμε ένα σημείο της, έστω  διάφορο του
διάφορο του  .
. γράψουμε κύκλο θα έχουμε την κατασκευή με κανόνα και διαβήτη.
γράψουμε κύκλο θα έχουμε την κατασκευή με κανόνα και διαβήτη. χρειάζεται λίγο προσοχή αφού θα πρέπει να γίνεται βέβαια με τρόπο που οι συντεταγμένες τους να αντιστοιχίζονται σε κατασκευάσιμα με κανόνα και διαβήτη ευθύγραμμα επί την αρχή τμήματα. Αν ας πούμε η εξίσωση της εφαπτομένης ήταν η
χρειάζεται λίγο προσοχή αφού θα πρέπει να γίνεται βέβαια με τρόπο που οι συντεταγμένες τους να αντιστοιχίζονται σε κατασκευάσιμα με κανόνα και διαβήτη ευθύγραμμα επί την αρχή τμήματα. Αν ας πούμε η εξίσωση της εφαπτομένης ήταν η  , τα πράγματα δεν είναι τα πλέον «ευοίωνα».
, τα πράγματα δεν είναι τα πλέον «ευοίωνα».Θα ήθελα να πώ ότι δεν μπορούμε πάντα να κατασκευάζουμε με κανόνα και διαβήτη μία ευθεία (με κλίση ας πούμεkostas_zervos έγραψε:Θα ήθελα η κατασκεύη να γίνει χωρίς την εξίσωση της εφαπτομενης γιατί τότε θα ξέρουμε την κλίση της και η ευθεία θα είναι κατασκευάσιμη....
 , διερχόμενη από την αρχή των αξόνων και με μονάδα μέτρησης δοθέν ευθύγραμμο τμήμα).
, διερχόμενη από την αρχή των αξόνων και με μονάδα μέτρησης δοθέν ευθύγραμμο τμήμα).
Ο Μαθηματικός αυτός προβληματισμός έχει ως Άριστη στόχευση την διμόρφωση Μαθηματικής μεθόδου και για τούτο τον θεωρώ σημαντικότατο.kostas_zervos έγραψε: Επίσης , αν είναι δυνατόν , μέσα πό τις κατασκευές να αναδειχτεί κάποια γενική ιδιότητα που μπορούν να έχουν (στη γενικής τους μορφή) πολλές από τις παραπάνω συναρτήσεις.
Ευχαριστώ....
 .
Ανάλυση:
.
Ανάλυση: είναι ημικύκλιο με κέντρο
είναι ημικύκλιο με κέντρο  και ακτίνα
και ακτίνα  που βρίσκεται από τον άξονα
που βρίσκεται από τον άξονα  και πάνω.
και πάνω. Ανάλυση:
Ανάλυση: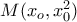 έχει εξίσωση
έχει εξίσωση 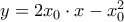 . Για
. Για  έχουμε
έχουμε  δηλαδή η εφαπτόμενη τέμνει τον
δηλαδή η εφαπτόμενη τέμνει τον 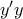 στο
στο 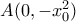 . Αν Β η προβολή του Μ στο
. Αν Β η προβολή του Μ στο 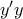 τότε
τότε  και τα Α , Β είναι συμμετρικά ως προς το Ο.
και τα Α , Β είναι συμμετρικά ως προς το Ο.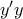 και βρίκουμε το συμμετρικό Α του Β ως προς το Ο. Τότε η ΑΜ είναι η εφαπτόμενη.
και βρίκουμε το συμμετρικό Α του Β ως προς το Ο. Τότε η ΑΜ είναι η εφαπτόμενη.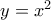 να διαπιστώσουμε ότι το σημείο
να διαπιστώσουμε ότι το σημείο 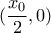 ανήκει στην αντίστοιχη εφαπτομένη
ανήκει στην αντίστοιχη εφαπτομένη  , οπότε το ενώνουμε το σημείο αυτό (που είναι σαφώς Κατασκευάσιμο) με το
, οπότε το ενώνουμε το σημείο αυτό (που είναι σαφώς Κατασκευάσιμο) με το  και έχουμε την κατασκευή της εφαπτομένης μας.
και έχουμε την κατασκευή της εφαπτομένης μας. (δίκην "τελίτσας"), αυτόματα έχουμε και την Γεωμετρική κατασκευή (κανόνας και διαβήτης) των ευθύγραμμων τμημάτων
(δίκην "τελίτσας"), αυτόματα έχουμε και την Γεωμετρική κατασκευή (κανόνας και διαβήτης) των ευθύγραμμων τμημάτων  όπου
όπου  οι προβολές του
οι προβολές του  στούς άξονες
στούς άξονες  αντίστοιχα.
αντίστοιχα. 
 συμβολίζουμε την αλγεβρική τιμή του
συμβολίζουμε την αλγεβρική τιμή του  .
.1. Διχοτομούμε το πρώτο και τρίτο τεταρτημόριο.kostas_zervos έγραψε: ↑Τετ Απρ 17, 2013 5:05 pmΜε δεδομένη τη γραφική παράσταση της συνάρτησης, να κατασκευαστεί (με κανόνα και διαβήτη) η εφαπτόμενη της
σε τυχαίο σημείο της
γ)
 . (Λάθος μου που δεν έβαλα σημείο στο σχήμα).
. (Λάθος μου που δεν έβαλα σημείο στο σχήμα).  και
και  , όπως φαίνεται παραπάνω.
, όπως φαίνεται παραπάνω. 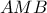 είναι η ζητούμενη.
είναι η ζητούμενη. τέμνει τον οριζόντιο άξονα στο σημείο με τη διπλάσια τετμημένη. Ναι, νομίζω κάτι τέτοιο ήθελε. Οπότε αρκεί να ενώσουμε το
τέμνει τον οριζόντιο άξονα στο σημείο με τη διπλάσια τετμημένη. Ναι, νομίζω κάτι τέτοιο ήθελε. Οπότε αρκεί να ενώσουμε το  με το
με το  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης