 . Να υπολογιστεί ο
. Να υπολογιστεί ο  .
.Συντονιστής: nsmavrogiannis
 . Να υπολογιστεί ο
. Να υπολογιστεί ο  .
.
Δεν νομίζω να είναι προφανές. Μάλιστα, ως απάντηση είναι λάθος.
 , η απάντηση είναι
, η απάντηση είναι  .
.  οταν ο
οταν ο  είναι ο μοναδικός πρώτος διαιρέτης του
είναι ο μοναδικός πρώτος διαιρέτης του  και
και  αλλιώς.
αλλιώς.
Τι νόημα έχει να δοθεί η απάντηση χωρίς λύση;Tolaso J Kos έγραψε: ↑Κυρ Αύγ 07, 2022 12:30 pmΤο αποτέλεσμα είναιοταν ο
είναι ο μοναδικός πρώτος διαιρέτης του
και
αλλιώς.
Έκανα λάθος.achilleas έγραψε: ↑Σάβ Αύγ 06, 2022 11:58 pmΔεν νομίζω να είναι προφανές. Μάλιστα, ως απάντηση είναι λάθος.
Π.χ. για, η απάντηση είναι
.
Καλό θα είναι να δίνονται πλήρεις λύσεις, σύμφωνα με τον κανονισμό του forum, ακόμα και για αποτελέσματα που φαίνονται προφανή.
 είναι πρώτος η απάντηση είναι
είναι πρώτος η απάντηση είναι  .
. είναι
είναι  το οποίο είναι ακέραιος, οπότε
το οποίο είναι ακέραιος, οπότε  . Τώρα το
. Τώρα το  είναι σχετικά πρώτος με το
είναι σχετικά πρώτος με το  , αφού το
, αφού το  είναι πρώτος, οπότε
είναι πρώτος, οπότε  από το οποίο έπεται ότι
από το οποίο έπεται ότι  .
. , το συμπέρασμα έπεται.
, το συμπέρασμα έπεται. και πρώτος
και πρώτος  . Αν ο
. Αν ο  δεν είναι δύναμη του
δεν είναι δύναμη του  , τότε
, τότε  .
. όπου
όπου  . Πρέπει
. Πρέπει  . Τότε
. Τότε  . Ο εκθέτης της μεγαλύτερης δύναμης του
. Ο εκθέτης της μεγαλύτερης δύναμης του  που διαιρεί το
που διαιρεί το  είναι ίσος με
είναι ίσος με 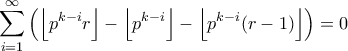
 έχουμε
έχουμε  ενώ για
ενώ για  έχουμε
έχουμε αφού
αφού  .
. 
 όπου
όπου  πρώτος, τότε
πρώτος, τότε  .
.  . Ο εκθέτης της μεγαλύτερης δύναμης του
. Ο εκθέτης της μεγαλύτερης δύναμης του  που διαιρεί το
που διαιρεί το  είναι ίσος με
είναι ίσος με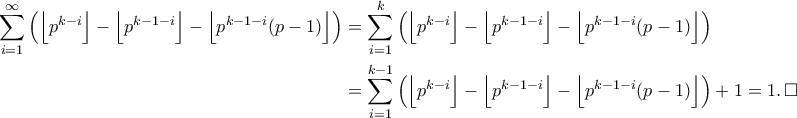
 όπου
όπου  πρώτος, τότε
πρώτος, τότε  .
. 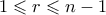 εκθέτης της μεγαλύτερης δύναμης του
εκθέτης της μεγαλύτερης δύναμης του  που διαιρεί το
που διαιρεί το  είναι ίσος με
είναι ίσος με
 ο όρος ισούται με
ο όρος ισούται με  .
. 
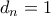 αν ο
αν ο  δεν είναι δύναμη πρώτου και
δεν είναι δύναμη πρώτου και  αν ο
αν ο  είναι δύναμη του πρώτου
είναι δύναμη του πρώτου  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες