Λογαριθμική άθροιση

M.S.Vovos · #1

Στην τάξη ο καθηγητής και ένας μαθητής κουβεντιάζουν, στο διάλλειμα.

M: Κύριε, θα ήθελα να ρωτήσω αν ισχύει $\ln(x+y)=\ln x+\ln y$ , για κάθε .
Κ: Όχι. Βρες δύο αριθμούς που να μην επαληθεύουν την παραπάνω ισότητα.
...O μαθητής σκέφτεται...
Μ: Ναι σωστά, π.χ. για και , δεν ισχύει.
Κ: Σωστά.
Μ: Ναι αλλά για ποιους θετικούς ακέραιους αριθμούς ισχύει αυτή η ισότητα;
K: Μμμ...Με μια γρήγορη ματιά βλέπω ότι η μόνη λύση είναι η .
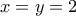Μ: Και πως αποδεικνύεται αυτό;
K: Άσκηση για το σπίτι, για την επόμενη φορά που έχουμε μάθημα.

Ισχύει ότι η μόνη θετική ακέραια λύση είναι το ζευγάρι ; Αν ναι, ποια απόδειξη σκέφτηκε ο καθηγητής;

Φιλικά,
Μάριος

Nikos127 · #2

Δεν είμαι σίγουρος αλλά ας κάνω μια προσπάθεια.
Θα δείξω ότι x=y=2

μοναδική λυση
Έχουμε: $ln(x+y)=lnx+lny, x,y\in \mathbb{N}^* \Rightarrow x+y=xy \Rightarrow x=\frac{y}{y-1} ,y\neq1$
Αν y=1

από αρχική σχέση η εξίσωση αδύνατη
Αν y=2

τότε

, η δοθείσα λυση.
Αρκεί να δείξω ότι $y/(y-1) \notin \mathbb{N}^*$ για $y\in\mathbb{N}^*-(1,2)$
Αν

περιττος τότε $y=2n+1, n\in \mathbb{N}^*$ οπότε $\frac{y}{y-1}=\frac{2n+1}{2n}=(1+\frac{1}{2n})\notin \mathbb{N}^*$
Αν

άρτιος τοτε $y=2m, m\in \mathbb{N}^*$ οποτε
$\frac{y}{y-1}=\frac{2m}{2m-1}=(1+\frac{1}{2m-1})\notin \mathbb{N}^*$ Ο.Ε.Δ.

Μάρκος Βασίλης · #3

Nikos127 έγραψε: ↑
Δευ Αύγ 24, 2020 3:02 pm
Δεν είμαι σίγουρος αλλά ας κάνω μια προσπάθεια.
Θα δείξω ότι μοναδική λυση
Έχουμε: $ln(x+y)=lnx+lny, x,y\in \mathbb{N}^* \Rightarrow x+y=xy \Rightarrow x=\frac{y}{y-1} ,y\neq1$
Αν από αρχική σχέση η εξίσωση αδύνατη
Αν τότε , η δοθείσα λυση.
Αρκεί να δείξω ότι $y/(y-1) \notin \mathbb{N}^*$ για $y\in\mathbb{N}^*-(1,2)$
Αν περιττος τότε $y=2n+1, n\in \mathbb{N}^*$ οπότε $\frac{y}{y-1}=\frac{2n+1}{2n}=(1+\frac{1}{2n})\notin \mathbb{N}^*$
Αν άρτιος τοτε $y=2m, m\in \mathbb{N}^*$ οποτε
$\frac{y}{y-1}=\frac{2m}{2m-1}=(1+\frac{1}{2m-1})\notin \mathbb{N}^*$ Ο.Ε.Δ.

Λίγο πιο απλά το σημείο που δείχνουμε ότι $\dfrac{y}{y-1}\not\in\mathbb{Z}_+$ για $y\in\mathbb{Z}_+\setminus\{1,2\}$ . Αν το $\frac{y}{y-1}$ είναι ακέραιος τότε το y-1

διαιρεί το

. Επειδή το y-1

διαιρεί και το y-1

έπεται ότι θα διαιρεί και το y-(y-1)=1

, άρα θα πρέπει y-1=1

, άρα

. Επίσης, για y=2

έχουμε $\dfrac{y}{y-1}=2$ , οπότε αποδείχθηκε το ζητούμενο.

User#0000 · #4

Καλησπέρα παραθέτω και την δική μου λύση λιγάκι διαφορετική.

ln(x+y)=lnx+lny

ή

,

Έστω

Άρα η σχέση (*)

γίνεται

, άτοπο.
Άρα y≠1

.
Επειδή το

είναι θετικός ακέραιος συνεπάγεται ότι
y≥2

Με όμοιο τρόπο αποδεικνύεται και ότι x≥2

Άρα η σχέση

γίνεται

Άρα

ή

Δηλαδή

οπότε

Επομένως αντικαθιστώντας στην σχέση

το

Καταλήγουμε σε x(1-2)=-2

ή

Δηλαδή η λύση της δοσμένης μας εξίσωσης είναι
(x,y)=(2,2)

Μάρκος Βασίλης · #5

Σε συνέχεια του #3, να δώσουμε και μία λύση με στοιχειώδη μέσα. Έστω x,y

θετικοί ακέραιοι τέτοιοι ώστε:

$\displaystyle{\\ln(x+y)=\ln x+\ln y\iff\ln(x+y)=\ln xy\iff x+y=x\ (\star)}$

Επομένως έπεται ότι ο

διαιρεί τον x+y

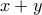, άρα και τον

. Ανάλογα, ο

διαιρεί τον x+y

άρα και τον

, επομένως $y=\pm x$ κι επειδή οι x,y

είναι αμφότεροι θετικοί έπεται ότι x=y

. Αντικαθιστώντας στην $(\star)$ έχουμε:

$\displaystyle{x+x=x^2\iff x^2-2x=0\iff x(x-2)=0\iff x=0\ \text{\gr ή }x=2,}$

κι επειδή x>0

έχουμε ότι x=y=2

.

Λογαριθμική άθροιση

Λογαριθμική άθροιση

Re: Λογαριθμική άθροιση

Re: Λογαριθμική άθροιση

Re: Λογαριθμική άθροιση

Re: Λογαριθμική άθροιση

Μέλη σε σύνδεση