Εξισωση

Ξένος · #1

Αν οι παρακατω αριθμοι ειναι τιμες μια εξισωσης

4
7
8

10
12
13
14
16
18
19
20
22
...
Μπορουμε να βρουμε με ποια εξισωση εκφραζονται?

Ξένος · #2

Δηλαδη βλεπουμε οτι αρχικα η τιμη αυξησης ειναι +3.
Μετα ακολουθει το μοτιβο +1 +2 +2 +1 επ'απειρον

KARKAR · #3

Ξένος έγραψε: ↑
Παρ Ιουν 12, 2020 9:37 pm
Αν οι παρακατω αριθμοι ειναι τιμες μια εξισωσης
........................................................
Μπορουμε να βρουμε με ποια εξισωση εκφραζονται?

Υποθέτω ότι θέλεις να ρωτήσεις το παρακάτω :

Αν οι αριθμοί ...................... είναι διαδοχικές τιμές μια ακολουθίας ,

μπορούμε να βρούμε ποια είναι η ακολουθία ;

Μια απάντηση θα μπορούσε να είναι η εξής : $a_{1}=4 , a_{2}=7$

και $a_{n}=\left\{\begin{matrix} a_{n-1}+1& n=3k , k\in \mathbb{N^*}\\ a_{n-1}+2& n\neq 3k , k\in \mathbb{N^*} \end{matrix}\right.$

Παρατήρηση : Θα μπορούσες τουλάχιστον να τονίζεις τις λέξεις !

#4

Το προηγούμενο δεν απαντά αλλά περιγράφει σωστότερα την ακολουθία. Αν θέλουμε τύπο, ο ακόλουθος είναι ένας.
a_1=4

και για $n\ge 2$ έχουμε

$\displaystyle{ a_n=\left\{\begin{matrix} 6k+1 & \alpha \nu \, n=4k-2\\ 6k+2 & \alpha \nu \, n=4k-1\\ 6k+4 & \alpha \nu \, n=4k\\ 6k+6 & \alpha \nu \, n=4k+1\\ \end{matrix}\right.}$

4ptil · #5

Ορίστε ένα πολυώνυμο που μηδενίζει για αυτές τις τιμές:
$P(x)=(\prod_{n=2}^{\propto }(x-4n-2))(\prod_{n=1}^{\propto }(x-4n))(\prod_{n=1}^{\propto }(x-6n- 1))$

#6

4ptil έγραψε: ↑
Σάβ Ιουν 13, 2020 11:10 am
Ορίστε ένα πολυώνυμο που μηδενίζει για αυτές τις τιμές:
$P(x)=(\prod_{n=2}^{\propto }(x-4n-2))(\prod_{n=1}^{\propto }(x-4n))(\prod_{n=1}^{\propto }(x-6n- 1))$

Μόνο που δεν είναι πολυώνυμο. Ακριβέστερα είναι παράσταση χωρίς νόημα.

Για παράδειγμα ποιος πραγματικός αριθμός ισούται με το P(1)

ή με το

ή με το $\displaystyle{P\left ( \frac {1}{2}\right )}$ ;

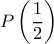Μόλις πάει κανείς να τα υπολογίσει, θα καταλάβει τι εννοώ όταν γράφω την πρώτη γραμμή παραπάνω. Το αφήνω για την ώρα.

4ptil · #7

Καταλαβαίνω ότι δεν είναι πολυώνυμο αφού δεν ακολουθεί τον ορισμό ενός πολυωνύμου αλλά πως είναι δυνατόν να κατασκευάσουμε εξίσωση με αυτές μόνο τις λύσεις διαφορετικά;

#8

4ptil έγραψε: ↑
Κυρ Ιουν 14, 2020 1:21 am
Καταλαβαίνω ότι δεν είναι πολυώνυμο αφού δεν ακολουθεί τον ορισμό ενός πολυωνύμου αλλά πως είναι δυνατόν να κατασκευάσουμε εξίσωση με αυτές μόνο τις λύσεις διαφορετικά;

Πολλές οι παρανοήσεις εδώ.

Πρώτον, όπως γράφω στο προηγούμενο μήνυμά μου, η παράσταση που γράφεις όχι μόνο δεν είναι πολυώνυμο αλλά δεν έχει καν νόημα.

Δεύτερον, το ότι ψάχνεις μία συνάρτηση που μηδενίζεται ακριβώς στα $4n,\, 4n+2,\, 6n+1$ δεν λύνει το πρόβλημα για δύο λόγους. Ο πρώτος είναι διότι δεν δίνει τις τιμές των a_n

(με λίγα λόγια είναι άσχετο θέμα). Ο δεύτερος είναι γιατί τα $4n,\, 4n+2,\, 6n+1$ δεν είναι οι θέσεις που ψάχνουμε (με λίγα λόγια, οι τιμές αυτές είναι άσχετες με την άσκηση).

Ας τα ξεχάσουμε αυτά. Από ότι καταλαβαίνω θέλεις μία συνάρτηση (όχι εξίσωση όπως την ονομάζεις) που να μηδενίζεται ακριβώς στα $4n,\, 4n+2,\, 6n+1$ . Μία τέτοια είναι η

$\displaystyle{ \sin \left (\frac {\pi}{4} x \right ) \cos \left (\frac {\pi}{4} x \right ) \cos \left (\frac {\pi}{6} x + \frac {\pi}{3}\right )}$ για x>0

4ptil · #9

δεν είχα σκευτεί τριγωνομετρικό κύκλο

Εξισωση

Εξισωση

Re: Εξισωση

Re: Εξισωση

Re: Εξισωση

Re: Εξισωση

Re: Εξισωση

Re: Εξισωση

Re: Εξισωση

Re: Εξισωση

Μέλη σε σύνδεση