μήπως μπορεί να δοθεί μια υπόδειξη ως προς το πως μπορούμε να δείξουμε ότι το
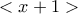 είναι πρώτο ιδεώδες στον δακτύλιο των πολυωνύμων με ακέραιους συντελεστές
είναι πρώτο ιδεώδες στον δακτύλιο των πολυωνύμων με ακέραιους συντελεστές ![Z[x] Z[x]](/forum/ext/geomar/texintegr/latexrender/pictures/b9cc39c52b08148c7eb8c4850888f5a6.png) ; Ευχαριστώ πολύ!
; Ευχαριστώ πολύ!Συντονιστής: nsmavrogiannis
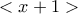 είναι πρώτο ιδεώδες στον δακτύλιο των πολυωνύμων με ακέραιους συντελεστές
είναι πρώτο ιδεώδες στον δακτύλιο των πολυωνύμων με ακέραιους συντελεστές ![Z[x] Z[x]](/forum/ext/geomar/texintegr/latexrender/pictures/b9cc39c52b08148c7eb8c4850888f5a6.png) ; Ευχαριστώ πολύ!
; Ευχαριστώ πολύ! με το
με το  .
.![\mathbb{Z}[x]/<x+1> \mathbb{Z}[x]/<x+1>](/forum/ext/geomar/texintegr/latexrender/pictures/3b925d5d6e4a0505354805dea77b2291.png) είναι ισόμορφος με τον
είναι ισόμορφος με τον  που προφανώς είναι ακέραια περιοχή.
που προφανώς είναι ακέραια περιοχή.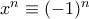 οπότε κάθε πολυώνυμο είναι ισοδύναμο με μια σταθερά. Επίσης, διαφορετικές σταθερές είναι μη ισοδύναμες οπότε προφανώς
οπότε κάθε πολυώνυμο είναι ισοδύναμο με μια σταθερά. Επίσης, διαφορετικές σταθερές είναι μη ισοδύναμες οπότε προφανώς ![\mathbb{Z}[x]/<x+1> \cong \mathbb{Z} \mathbb{Z}[x]/<x+1> \cong \mathbb{Z}](/forum/ext/geomar/texintegr/latexrender/pictures/8b5878c6ede7f0a36414d4d288d84095.png) .
.![\mathbb{Z}[x]/<x+1> \mathbb{Z}[x]/<x+1>](/forum/ext/geomar/texintegr/latexrender/pictures/3b925d5d6e4a0505354805dea77b2291.png) ), τότε ουσιαστικά είναι σαν να ταυτίζουμε το
), τότε ουσιαστικά είναι σαν να ταυτίζουμε το  με το
με το  .
.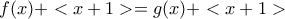 αν και μόνο αν
αν και μόνο αν  .
. δηλαδή ταυτίσαμε το
δηλαδή ταυτίσαμε το  με το
με το  .
. αν και μόνο αν
αν και μόνο αν  .
. με το
με το  .
. έχουμε
έχουμε  .
. μπορούμε να δούμε ότι
μπορούμε να δούμε ότι 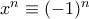 και επειδή ένα πολυώνυμο είναι συνδυασμός δυνάμεων του
και επειδή ένα πολυώνυμο είναι συνδυασμός δυνάμεων του  παίρνουμε ότι κάθε πολυώνυμο είναι ισοδύναμο με ένα σταθερό πολυώνυμο.
παίρνουμε ότι κάθε πολυώνυμο είναι ισοδύναμο με ένα σταθερό πολυώνυμο. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες