 με πραγματικούς συντελεστές και
με πραγματικούς συντελεστές και  .
.Στόχος της ανάρτησης είναι να συγκεντρωθούν προς χάριν των συναδέλφων, διάφορες διδάξιμες τεχνικές επίλυσης.
Συντονιστής: nsmavrogiannis
 με πραγματικούς συντελεστές και
με πραγματικούς συντελεστές και  .
.Καλημέρα!nsmavrogiannis έγραψε: ↑Κυρ Απρ 05, 2020 12:52 amΝα λυθεί η εξίσωσημε πραγματικούς συντελεστές και
.
Στόχος της ανάρτησης είναι να συγκεντρωθούν προς χάριν των συναδέλφων, διάφορες διδάξιμες τεχνικές επίλυσης.
 Πολλαπλασιάζω και τα δύο μέλη με
Πολλαπλασιάζω και τα δύο μέλη με  και προσθέτω το
και προσθέτω το 

 με την προϋπόθεση ότι
με την προϋπόθεση ότι  Πιο συγκεκριμένα:
Πιο συγκεκριμένα: Αν
Αν  τότε έχουμε δύο ρίζες πραγματικές και άνισες
τότε έχουμε δύο ρίζες πραγματικές και άνισες 
 Αν
Αν  τότε έχουμε μία διπλή ρίζα
τότε έχουμε μία διπλή ρίζα 
 Αν
Αν  τότε έχουμε δύο ρίζες μιγαδικές συζυγείς
τότε έχουμε δύο ρίζες μιγαδικές συζυγείς 
α) Αν η εξίσωση είχε την μορφήnsmavrogiannis έγραψε: ↑Κυρ Απρ 05, 2020 12:52 amΝα λυθεί η εξίσωσημε πραγματικούς συντελεστές και
.
Στόχος της ανάρτησης είναι να συγκεντρωθούν προς χάριν των συναδέλφων, διάφορες διδάξιμες τεχνικές επίλυσης.
 (ισοδύναμα
(ισοδύναμα  ) θα μπορούσα να την λύσω και διερευνήσω εύκολα.
) θα μπορούσα να την λύσω και διερευνήσω εύκολα. . Συγκεκριμένα θα γίνει
. Συγκεκριμένα θα γίνει , ισοδύναμα
, ισοδύναμα  . Οπότε επιλέγουμε
. Οπότε επιλέγουμε  ή
ή  .
. οι ρίζες της εξίσωσης. Τότε:
οι ρίζες της εξίσωσης. Τότε: Άρα:
Άρα: και
και  απ' όπου
απ' όπου 
 θα είναι
θα είναι  και από
και από 

 The Mathematical Gazette, Vol. 42, No. 339 (Feb., 1958), σ. 65
The Mathematical Gazette, Vol. 42, No. 339 (Feb., 1958), σ. 65
 έχουμε την ισοδύναμη εξίσωση
έχουμε την ισοδύναμη εξίσωση
 έχουν άθροισμα
έχουν άθροισμα  επομένως ο αριθμός
επομένως ο αριθμός  είναι το μέσον του διαστήματος που ορίζουν αν είναι διαφορετικοί και ίσος με αυτούς αν είναι ίσοι. Επομένως θα υπάρχει αριθμός
είναι το μέσον του διαστήματος που ορίζουν αν είναι διαφορετικοί και ίσος με αυτούς αν είναι ίσοι. Επομένως θα υπάρχει αριθμός  θετικός ή αρνητικός ώστε ο πρώτος να είναι
θετικός ή αρνητικός ώστε ο πρώτος να είναι  και ο δεύτερος
και ο δεύτερος  . Το γινόμενο τους είναι
. Το γινόμενο τους είναι  επομένως
επομένως 


 και σε αυτή την περίπτωση
και σε αυτή την περίπτωση 

 .
.Καλησπέρα σε όλουςsilouan έγραψε: ↑Δευ Απρ 06, 2020 9:16 pmΔείτε και εδώ:
viewtopic.php?f=6&t=65828&p=318796&hili ... en#p318796
 θα έχει λύση
θα έχει λύση  αν και μόνο αν
αν και μόνο αν  ,
, ισχύει
ισχύει  δηλαδή αν και μόνο αν για κάθε
δηλαδή αν και μόνο αν για κάθε  είναι
είναι  .
. αν και μόνο αν έχει λύση και τον αριθμό
αν και μόνο αν έχει λύση και τον αριθμό  . Οι αριθμοί αυτοί, που ενδεχομένως είναι ίσοι, έχουν ημιάθροισμα
. Οι αριθμοί αυτοί, που ενδεχομένως είναι ίσοι, έχουν ημιάθροισμα  και επομένως υπάρχει αριθμός
και επομένως υπάρχει αριθμός  (θετικός αρνητικός ή μηδέν) ώστε
(θετικός αρνητικός ή μηδέν) ώστε  και η εξίσωση θα έχει ρίζα
και η εξίσωση θα έχει ρίζα  αν και μόνο αν
αν και μόνο αν  ή ισοδύναμα αν
ή ισοδύναμα αν  δηλαδή αν και μόνο αν υπάρχει
δηλαδή αν και μόνο αν υπάρχει  ώστε
ώστε  .
. και οι λύσεις θα είναι
και οι λύσεις θα είναι  δηλαδή
δηλαδή  .
. της εξίσωσης
της εξίσωσης  ,
, 


 , καθώς
, καθώς  .
.  η ισότητα
η ισότητα 
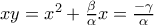 .
.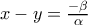 και
και  .
. και
και  στην ταυτότητα
στην ταυτότητα 
 (*),
(*), από την (*) ισοδύναμα παίρνουμε
από την (*) ισοδύναμα παίρνουμε  ή
ή .
.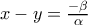
 ή
ή  ,
, ,
,  αν
αν  ενώ
ενώ  αν
αν  .
. γίνεται και στην μέθοδο Lagrange resolvents π.χ. στην ενότητα 4.3 "By Lagrange resolvents".
γίνεται και στην μέθοδο Lagrange resolvents π.χ. στην ενότητα 4.3 "By Lagrange resolvents".Καταρχάς χρόνια πολλά με υγεία σε όλους!Mihalis_Lambrou έγραψε: ↑Κυρ Απρ 05, 2020 12:25 pmα) Αν η εξίσωση είχε την μορφήnsmavrogiannis έγραψε: ↑Κυρ Απρ 05, 2020 12:52 amΝα λυθεί η εξίσωσημε πραγματικούς συντελεστές και
.
Στόχος της ανάρτησης είναι να συγκεντρωθούν προς χάριν των συναδέλφων, διάφορες διδάξιμες τεχνικές επίλυσης.(ισοδύναμα
) θα μπορούσα να την λύσω και διερευνήσω εύκολα.
β) Γενικά τώρα, μπορούμε να φέρουμε την εξίσωση στην παραπάνω μορφή κάνοντας μετασχηματισμό της μορφής. Συγκεκριμένα θα γίνει
, ισοδύναμα
. Οπότε επιλέγουμε
ή
.
Και λοιπά.
 στη γενική μορφή, θέτοντας όπου
στη γενική μορφή, θέτοντας όπου  , λαμβάνουμε μία νέα εξίσωση στην οποία έχει γίνει απαλοιφή του όρου:
, λαμβάνουμε μία νέα εξίσωση στην οποία έχει γίνει απαλοιφή του όρου:  .
.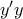 στις πρωτοβάθμιες ή η κορυφή της παραβολής να έρθει στον
στις πρωτοβάθμιες ή η κορυφή της παραβολής να έρθει στον 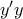 αντίστοιχα στις δευτεροβάθμιες. Δηλαδή έχει ενδιαφέρον να δούμε πώς δρα ο μετασχηματισμός και στις πρωτοβάθμιες εξισώσεις:
αντίστοιχα στις δευτεροβάθμιες. Δηλαδή έχει ενδιαφέρον να δούμε πώς δρα ο μετασχηματισμός και στις πρωτοβάθμιες εξισώσεις: . Ο μετασχηματισμός είναι σε αυτήν την περίπτωση:
. Ο μετασχηματισμός είναι σε αυτήν την περίπτωση:  και θέτοντας στην αρχιική εξίσωση έχουμε:
και θέτοντας στην αρχιική εξίσωση έχουμε: 
 .
.
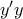 , αφού πετυχαίνει να γίνει
, αφού πετυχαίνει να γίνει  δηλαδή
δηλαδή  .
.

Χριστός Ανέστηchris_gatos έγραψε: ↑Παρ Απρ 17, 2020 2:36 amΚαλημέρα!
Μιας και είδα τη δημοσίευση και μου ήρθε στο μυαλό μια μέθοδο που είχα διαβάσει παλαιότερα
στο περιοδικό "εκπαιδευτικοί προβληματισμοί" του οποίου τα τεύχη παρέχονται on line.
Το άρθρο που παραπέμπω είναι του Ανδρέα Σβέρκου και μιλά για γραφική επίλυση εξίσωσης
2ου βαθμού με τη βοήθεια κύκλου.
3ο τεύχος "Εκπαιδευτικοί προβληματισμοί.
 , The Mathematical Gazette 42, No 339, 1958 σελ. 57
, The Mathematical Gazette 42, No 339, 1958 σελ. 57 .
. . Ο τρόπος, αδρομερώς, είναι ο ακόλουθος:
. Ο τρόπος, αδρομερώς, είναι ο ακόλουθος: ,
,  και με διάμετρο αυτά τα σημεία γράφεται κύκλος. Οι τετμημένες των σημείων τομής του κύκλου αυτού με τον
και με διάμετρο αυτά τα σημεία γράφεται κύκλος. Οι τετμημένες των σημείων τομής του κύκλου αυτού με τον  -άξονα, εφ' όσον υπάρχουν, είναι οι ρίζες.
-άξονα, εφ' όσον υπάρχουν, είναι οι ρίζες.
 -άξονα.
Αν πρόκειται το θέμα να διδαχθεί στην Β΄Λυκείου αντί της εξίσωσης του κύκλου μπορεί να χρησιμοποιηθεί εσωτερικό γινόμενο διανυσμάτων που μας δίνει κατ΄ευθείαν
-άξονα.
Αν πρόκειται το θέμα να διδαχθεί στην Β΄Λυκείου αντί της εξίσωσης του κύκλου μπορεί να χρησιμοποιηθεί εσωτερικό γινόμενο διανυσμάτων που μας δίνει κατ΄ευθείαν  δηλαδή
δηλαδή  .
. στην μορφή
στην μορφή  απ΄οτην στιγμή που δουλεύουμε με άξονες έχουμε μοναδιαίο τμήμα και μπορούμε να κατασκευάσουμε τους αριθμούς
απ΄οτην στιγμή που δουλεύουμε με άξονες έχουμε μοναδιαίο τμήμα και μπορούμε να κατασκευάσουμε τους αριθμούς  αρκεί να έχουμε τους αριθμούς
αρκεί να έχουμε τους αριθμούς 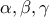 . Για να βρούμε λ.χ. το
. Για να βρούμε λ.χ. το  από το σημείο
από το σημείο  παράλληλη στο τμήμα των
παράλληλη στο τμήμα των  και
και  η οποία τέμενει τον άξονα των
η οποία τέμενει τον άξονα των  στο
στο 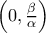 .
Η αναγωγή της γενικής περίπτωσης στην ειδική έπεται.
.
Η αναγωγή της γενικής περίπτωσης στην ειδική έπεται.Σωστά.nsmavrogiannis έγραψε: ↑Κυρ Απρ 19, 2020 9:24 pmΦυσικά είναι λογικό για τόσο "ψαγμένα" θέματα να υπάρχουν κάπου στο παρελθόν οι ίδιeς επεξεργασίες.
 . Παραθέτω το αρθράκι και όχι τις πρωτότυπες πηγές γιατί είναι ευχάριστο και απλό ανάγνωσμα στο αρχικό ερώτημα του θρεντ, σίγουρα προσιτό σε μαθητές που ξέρουν αγγλικά.
. Παραθέτω το αρθράκι και όχι τις πρωτότυπες πηγές γιατί είναι ευχάριστο και απλό ανάγνωσμα στο αρχικό ερώτημα του θρεντ, σίγουρα προσιτό σε μαθητές που ξέρουν αγγλικά. . Περιέχεται στην πρόταση ια' από το 2ο βιβλίο του Ευκλείδη, όπως την παρουσιάζει ο Γιώργος Λαγουδάκος στο βιβλίο του Στιγμές Ιστορίας της Επίλυσης των εξισώσεων. (Η διαδικτυακή αναζήτηση είναι εύκολη).
. Περιέχεται στην πρόταση ια' από το 2ο βιβλίο του Ευκλείδη, όπως την παρουσιάζει ο Γιώργος Λαγουδάκος στο βιβλίο του Στιγμές Ιστορίας της Επίλυσης των εξισώσεων. (Η διαδικτυακή αναζήτηση είναι εύκολη).Μιχάλη πράγματι ο Καρτέσιος αναφέρει την τεχνική αυτή στην Γεωμετρία του (Στην έκδοση Dover που έχω είναι στις σελίδες 12-13). Στο κείμενο δεν αναφέρεται πως προκύτει το συμπέρασμα. Οι μεταφραστές-επιμελητές (μεταξύ των οποίων και ο Smith) εικάζουν (υποσημείωση της σελίδας 13) ότι χρησιμοποιεί αυτό που ονομάστηκε αργότερα "δύναμη σημείου". Το αποτέλεσμα υπάρχει στα "Στοιχεία" (είναι η 36 του τρίτου βιβλίου) και αναλύεται πολύ ωραία στοMihalis_Lambrou έγραψε: ↑Κυρ Απρ 19, 2020 10:44 pmΣωστά.nsmavrogiannis έγραψε: ↑Κυρ Απρ 19, 2020 9:24 pmΦυσικά είναι λογικό για τόσο "ψαγμένα" θέματα να υπάρχουν κάπου στο παρελθόν οι ίδιeς επεξεργασίες.
Η μέθοδος που παραθέτει ο Γιώργος παραπάνω (ποστ #10) από το Σχολικό βιβλίο, οφείλεται στον Descart. Την έχει κοντά στην αρχή της περίφημης La Geometrie του.
Ωραία μέθοδο γεωμετρικής ερμηνείας της συμπλήρωσης τετραγώνου είχε στην δική του Άλγεβρα ο Al Kwarizmi.
Και τα δύο υπάρχουν εν γένει στις καλές ιστορίες των Μαθηματικών αλλά τις περιέχει και το αρθράκι
εδώ
στην σελίδα. Παραθέτω το αρθράκι και όχι τις πρωτότυπες πηγές γιατί είναι ευχάριστο και απλό ανάγνωσμα στο αρχικό ερώτημα του θρεντ, σίγουρα προσιτό σε μαθητές που ξέρουν αγγλικά.
Γιώργο ευχαριστούμε.Γιώργος Ρίζος έγραψε: ↑Δευ Απρ 20, 2020 11:49 am....
Ως συνέχεια της ενδιαφέρουσας συζήτησης, δίνω μια ειδική περίπτωση γεωμετρικής επίλυσης δευτεροβάθμιάς εξίσωσης, της μορφής. Περιέχεται στην πρόταση ια' από το 2ο βιβλίο του Ευκλείδη, όπως την παρουσιάζει ο Γιώργος Λαγουδάκος στο βιβλίο του Στιγμές Ιστορίας της Επίλυσης των εξισώσεων. (Η διαδικτυακή αναζήτηση είναι εύκολη).
....
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες