 ώστε
ώστε 
για κάθε
 μη αρνητικούς πραγματικούς.
μη αρνητικούς πραγματικούς.Συντονιστής: nsmavrogiannis
 ώστε
ώστε 
 μη αρνητικούς πραγματικούς.
μη αρνητικούς πραγματικούς. θα ισχύει και για τους
θα ισχύει και για τους  όπου
όπου 
 (την γράφουμε έτσι για να μην έχουμε σκοτούρες με το
(την γράφουμε έτσι για να μην έχουμε σκοτούρες με το  )
)
 και με τη στάνταρ διαδικασία βρίσκουμε
και με τη στάνταρ διαδικασία βρίσκουμε  .
.
 ισχύει
ισχύει
 και
και  , οπότε αναζητούμε το ελάχιστο της
, οπότε αναζητούμε το ελάχιστο της
 και
και 

 (*)
(*)
 , άρα αρκει να αποδειχθεί η ανισότητα που προέκυψε για
, άρα αρκει να αποδειχθεί η ανισότητα που προέκυψε για  και
και  &
&  : αυτή ισχύει 'τριωνυμικώς' λόγω των ανισοτήτων
: αυτή ισχύει 'τριωνυμικώς' λόγω των ανισοτήτων
 , η δεύτερη είναι ισοδύναμη προς την
, η δεύτερη είναι ισοδύναμη προς την  ... που ισχύει για
... που ισχύει για  καθώς
καθώς  και
και  .]
.] και από την
και από την  .
. για
για  ισούται προς
ισούται προς  .
. και την
και την
 ελαχιστοποιείται στο δοθέν διάστημα για
ελαχιστοποιείται στο δοθέν διάστημα για  , και το ζητούμενο ελάχιστο ισούται προς
, και το ζητούμενο ελάχιστο ισούται προς
 για τον οποίο ισχύει η
για τον οποίο ισχύει η  είναι λοιπόν ο
είναι λοιπόν ο  , με την ισότητα να επιτυγχάνεται για
, με την ισότητα να επιτυγχάνεται για  ,
,  ,
,  .
.Αν και το πρόβλημα έχει καλυφθεί πλήρως ... θα ήθελα να δείξω πως κατέληξα 'κατασκευαστικώς' στα παραπάνω ΠΡΙΝ το λύσω:
 , αναζητούμε -- παρατηρώντας ότι
, αναζητούμε -- παρατηρώντας ότι  -- εκείνα τα
-- εκείνα τα  για τα οποία αυτή θα είναι αύξουσα, θα ισχύει δηλαδή η
για τα οποία αυτή θα είναι αύξουσα, θα ισχύει δηλαδή η ![f'(c)\geq 0\leftrightarrow 3c^2-3ab-m(a-b)[-(c-a)+(b-c)]\geq 0\leftrightarrow 3c^2-3ab+m(b-a)(a+b-2c)\geq 0. f'(c)\geq 0\leftrightarrow 3c^2-3ab-m(a-b)[-(c-a)+(b-c)]\geq 0\leftrightarrow 3c^2-3ab+m(b-a)(a+b-2c)\geq 0.](/forum/ext/geomar/texintegr/latexrender/pictures/007554bfd5001adc5abf6ad447d9deb2.png)
 , αναζητούμε -- παρατηρώντας ότι
, αναζητούμε -- παρατηρώντας ότι  -- εκείνα τα
-- εκείνα τα  για τα οποία
για τα οποία 
 .
. για
για  , άρα
, άρα  . [Είναι πιθανή η
. [Είναι πιθανή η  καθώς για
καθώς για  είναι δυνατόν να είναι θετική η
είναι δυνατόν να είναι θετική η  για
για  χωρίς να είναι αύξουσα.]
χωρίς να είναι αύξουσα.] ,
, 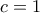 , η ζητούμενη λαμβάνει την μορφή
, η ζητούμενη λαμβάνει την μορφή  , όπου
, όπου  . Για να έχουμε όμως το μέγιστο δυνατό
. Για να έχουμε όμως το μέγιστο δυνατό  θα πρέπει να ισχύει και η
θα πρέπει να ισχύει και η  , δηλαδή η
, δηλαδή η 
 λαμβάνουμε την εξίσωση
λαμβάνουμε την εξίσωση
 , άρα
, άρα  . [Ήταν ακόμη πιθανή η
. [Ήταν ακόμη πιθανή η  , καθώς δεν είχα ακόμη αποδείξει ότι για μέγιστο
, καθώς δεν είχα ακόμη αποδείξει ότι για μέγιστο  οφείλουμε να έχουμε
οφείλουμε να έχουμε  .]
.] ,
,  διαπιστώνουμε ότι μπορούμε να υποθέσουμε
διαπιστώνουμε ότι μπορούμε να υποθέσουμε  : αυτό μπορεί να γίνει μέσω της ανισότητας
: αυτό μπορεί να γίνει μέσω της ανισότητας 
 μπορούμε πλέον να υποθέσουμε
μπορούμε πλέον να υποθέσουμε  , οπότε αναζητούμε εκείνο το
, οπότε αναζητούμε εκείνο το  για το οποίο η
για το οποίο η  εφάπτεται του άξονα των
εφάπτεται του άξονα των  (
( ), όπως έγινε στο #7, Ή έχει διπλή ρίζα: σ' αυτήν την προσέγγιση η
), όπως έγινε στο #7, Ή έχει διπλή ρίζα: σ' αυτήν την προσέγγιση η  μας δίνει το σύστημα
μας δίνει το σύστημα  ,
,  ,
,  , οπότε προκύπτουν οι
, οπότε προκύπτουν οι  ,
, 


gbaloglou έγραψε: ↑Δευ Ιαν 20, 2020 8:08 pmΠαρατηρώ, ότι συνδυάζοντας ιδέες από τις δύο προηγούμενες δημοσιεύσεις (#6 & #7), μπορούμε να αποφύγουμε πλήρως την χρήση παραγώγων και επομένως να παραμείνουμε 100% εντός φακέλου:
Μέσω της αναγωγής,
διαπιστώνουμε ότι μπορούμε να υποθέσουμε
: αυτό μπορεί να γίνει μέσω της ανισότητας
που μπορεί να αποδειχθεί ΚΑΙ χωρίς την χρήση παραγώγων (#6). Έχοντας τώρα κάνει την αναγωγήμπορούμε πλέον να υποθέσουμε
, οπότε αναζητούμε εκείνο το
για το οποίο η
εφάπτεται του άξονα των
(
), όπως έγινε στο #7, Ή έχει διπλή ρίζα: σ' αυτήν την προσέγγιση η
μας δίνει το σύστημα
,
,
, οπότε προκύπτουν οι
,
από τις πρώτες δύο εξισώσεις και από την τρίτη εξίσωση προκύπτει η γνωστή (#7)
Η 'τελική' αυτή εξίσωση επιλύεται πολύ πιο εύκολα από την αντίστοιχη 'τελική' εξίσωση στην #6, καθώς ανάγεται στην διτετράγωνη

 ώστε
ώστε 
 με
με  . Οπότε αρκεί
. Οπότε αρκεί
 , αρκεί
, αρκεί 
 , η τελευταία ανάγεται στην ανισότητα μιας μεταβλητής
, η τελευταία ανάγεται στην ανισότητα μιας μεταβλητής
 και με την παράγωγο βρίσκουμε ότι είναι θετικό αν και μόνο αν
και με την παράγωγο βρίσκουμε ότι είναι θετικό αν και μόνο αν  , οπότε φτάνουμε στη διτρετράγωνη που βρήκε και ο κ. Μπαλόγλου παραπάνω.
, οπότε φτάνουμε στη διτρετράγωνη που βρήκε και ο κ. Μπαλόγλου παραπάνω.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες