Γιώργο πολύ ωραία, ευχαριστώ. Να επισημάνω εδώ ότι για

η ακολουθία που ορίζεται από την ανάδραση (iteration)

ΣΥΓΚΛΙΝΕΙ (προς ένα και μοναδικό όριο δηλαδή, και αυτό δεν είναι άλλο από το

, λύση της 'εξίσωσης σύγκλισης'

που προκύπτει άμεσα από την παραπάνω ανάδραση). [Το ίδιο και για

, όπου οι τρεις μη τετριμμένες ρίζες συμπίπτουν.]
Έχουμε δηλαδή το εξής πολύ ενδιαφέρον, και όχι πλήρως κατανοητό εκ μέρους μου, φαινόμενο: το όριο

που προκύπτει για
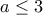
, από την απλή ανάδραση

, 'επιζεί' ως ρίζα της 'εξίσωσης σύγκλισης'
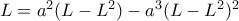
που προκύπτει από την διπλή ανάδραση

,

(μέσω αντικατάστασης της δεύτερης σχέσης στην πρώτη)^ για

* η διπλή αυτή ανάδραση οδηγεί, όπως είχα γράψει εξ αρχής, σε ΔΥΟ συγκλίνουσες υπακολουθίες (τα όρια των οποίων ταυτίζονται με τις ρίζες του τριωνύμου που προκύπτει ύστερα από την διαίρεση του 'αρχικού' πολυωνύμου δια

και δια

).
*Λίγο πιο κάτω από το

αρχίζουμε, 'για λίγο', να έχουμε ΤΕΣΣΕΡΑ όρια αντί για δύο, καθώς η 'εξίσωση σύγκλισης' 16ου βαθμού** που προκύπτει από τετραπλή πλέον ανάδραση αρχίζει να έχει ΟΚΤΩ πραγματικές ρίζες (τρεις από τις οποίες είναι αυτές που ήδη γνωρίζουμε από τις περιπτώσεις απλής και διπλής ανάδρασης, και που 'επιζούν'). (Όγδοη πραγματική ρίζα η

, εννοείται

) [Λίγο πιο πάνω αρχίζουμε να έχουμε 8 όρια, ακόμη συντομότερα 16, κοκ, ώσπου γύρω στο

αρχίζει το ΧΑΟΣ, και εκλείπει κάθε έννοια σύγκλισης και περιοδικότητας!]
**Ένας τρόπος να γραφεί αυτή -- ώστε να χωράει στην διαδικτυακή εκδοχή του WolframAlpha αν μη τι άλλο -- είναι:


 .
. ,
,  ΚΑΙ την υπόθεση διπλής σύγκλισης της ακολουθίας
ΚΑΙ την υπόθεση διπλής σύγκλισης της ακολουθίας  , την ύπαρξη δηλαδή ΔΥΟ υπακολουθιών που συγκλίνουν σε διαφορετικά όρια. Υποθέτουμε ότι
, την ύπαρξη δηλαδή ΔΥΟ υπακολουθιών που συγκλίνουν σε διαφορετικά όρια. Υποθέτουμε ότι  , άρα και οι λύσεις της παραπάνω τεταρτοβάθμιας που προκύπτει οφείλουν, πλην της προφανούς
, άρα και οι λύσεις της παραπάνω τεταρτοβάθμιας που προκύπτει οφείλουν, πλην της προφανούς  , να κείνται στο
, να κείνται στο  . (Δύο από τις τρεις μη προφανείς λύσεις είναι τα ζητούμενα όρια.)]
. (Δύο από τις τρεις μη προφανείς λύσεις είναι τα ζητούμενα όρια.)]
![\displaystyle x\left[ {{a^3}x{{(x - 1)}^2} + {a^2}(x - 1) + 1} \right] = 0 \displaystyle x\left[ {{a^3}x{{(x - 1)}^2} + {a^2}(x - 1) + 1} \right] = 0](/forum/ext/geomar/texintegr/latexrender/pictures/f49dcb3147b4ab5cde45a1c28c1261e7.png) και μία λύση είναι η
και μία λύση είναι η 
 και έχω:
και έχω:
 τότε
τότε 
 ή
ή 
 Η τελευταία αυτή εξίσωση έχει πραγματικές ρίζες αν
Η τελευταία αυτή εξίσωση έχει πραγματικές ρίζες αν 
 η ακολουθία που ορίζεται από την ανάδραση (iteration)
η ακολουθία που ορίζεται από την ανάδραση (iteration)  , λύση της 'εξίσωσης σύγκλισης'
, λύση της 'εξίσωσης σύγκλισης'  που προκύπτει άμεσα από την παραπάνω ανάδραση). [Το ίδιο και για
που προκύπτει άμεσα από την παραπάνω ανάδραση). [Το ίδιο και για  , όπου οι τρεις μη τετριμμένες ρίζες συμπίπτουν.]
, όπου οι τρεις μη τετριμμένες ρίζες συμπίπτουν.]  που προκύπτει για
που προκύπτει για 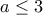 , από την απλή ανάδραση
, από την απλή ανάδραση 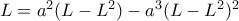 που προκύπτει από την διπλή ανάδραση
που προκύπτει από την διπλή ανάδραση  * η διπλή αυτή ανάδραση οδηγεί, όπως είχα γράψει εξ αρχής, σε ΔΥΟ συγκλίνουσες υπακολουθίες (τα όρια των οποίων ταυτίζονται με τις ρίζες του τριωνύμου που προκύπτει ύστερα από την διαίρεση του 'αρχικού' πολυωνύμου δια
* η διπλή αυτή ανάδραση οδηγεί, όπως είχα γράψει εξ αρχής, σε ΔΥΟ συγκλίνουσες υπακολουθίες (τα όρια των οποίων ταυτίζονται με τις ρίζες του τριωνύμου που προκύπτει ύστερα από την διαίρεση του 'αρχικού' πολυωνύμου δια  και δια
και δια  ).
).  αρχίζουμε, 'για λίγο', να έχουμε ΤΕΣΣΕΡΑ όρια αντί για δύο, καθώς η 'εξίσωση σύγκλισης' 16ου βαθμού** που προκύπτει από τετραπλή πλέον ανάδραση αρχίζει να έχει ΟΚΤΩ πραγματικές ρίζες (τρεις από τις οποίες είναι αυτές που ήδη γνωρίζουμε από τις περιπτώσεις απλής και διπλής ανάδρασης, και που 'επιζούν'). (Όγδοη πραγματική ρίζα η
αρχίζουμε, 'για λίγο', να έχουμε ΤΕΣΣΕΡΑ όρια αντί για δύο, καθώς η 'εξίσωση σύγκλισης' 16ου βαθμού** που προκύπτει από τετραπλή πλέον ανάδραση αρχίζει να έχει ΟΚΤΩ πραγματικές ρίζες (τρεις από τις οποίες είναι αυτές που ήδη γνωρίζουμε από τις περιπτώσεις απλής και διπλής ανάδρασης, και που 'επιζούν'). (Όγδοη πραγματική ρίζα η  , εννοείται
, εννοείται  αρχίζει το ΧΑΟΣ, και εκλείπει κάθε έννοια σύγκλισης και περιοδικότητας!]
αρχίζει το ΧΑΟΣ, και εκλείπει κάθε έννοια σύγκλισης και περιοδικότητας!]
