Ορίζεται η δύναμη
 ;
;Συντονιστής: nsmavrogiannis
![\displaystyle
- 8 = \left( { - 2} \right)^3 = \left( { - 2} \right)^{\frac{6}{2}} = \left[ {\left( { - 2} \right)^6 } \right]^{\frac{1}{2}} = 64^{\frac{1}{2}} = \sqrt {64} = 8
\displaystyle
- 8 = \left( { - 2} \right)^3 = \left( { - 2} \right)^{\frac{6}{2}} = \left[ {\left( { - 2} \right)^6 } \right]^{\frac{1}{2}} = 64^{\frac{1}{2}} = \sqrt {64} = 8](/forum/ext/geomar/texintegr/latexrender/pictures/f88088aceb57ba9198b06ee55c6052b1.png)
 .
.


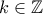 είναι
είναι 
Τελικά το λάθος είναι στο δεύτερο "=" που περνάμε σε κλασματικό εκθέτη, ή στο τρίτο "=" που χρησιμοποιούμε την ιδιότητα δύναμης σε άλλη δύναμη;
H εκθέτες όλοι πάνε μόνο στοΓιάννης Θωμαΐδης έγραψε: ↑Τετ Νοέμ 01, 2017 8:48 pmΝα βρείτε το λάθος στην παρακάτω «απόδειξη» της ισότητας –8 = 8:
 και όχι στο
και όχι στο  . Η πρώτη ισότητα απλά ισχύει επειδή ο
. Η πρώτη ισότητα απλά ισχύει επειδή ο  είναι περιττός ένα παράδειγμα
είναι περιττός ένα παράδειγμα 
![-8=(-2)^{3}=(-2)^{\frac{6}{2}}=[(-2)^{6}]^{\frac{1}{2}}=64^{\frac{1}{2}}=\sqrt{64}=8 -8=(-2)^{3}=(-2)^{\frac{6}{2}}=[(-2)^{6}]^{\frac{1}{2}}=64^{\frac{1}{2}}=\sqrt{64}=8](/forum/ext/geomar/texintegr/latexrender/pictures/0f6111854f47dcc4515bbd66f9c98263.png)
 , δεδομένου ότι
, δεδομένου ότι  , και τότε φυσικά δεν υπάρχει κανένα παράδοξο. Όμως το δίτιμο σύμβολο της τετραγωνικής ρίζας, που ήταν απολύτως νόμιμο και σεβαστό επί αιώνες και χρησιμοποιήθηκε με δεξιοτεχνία από μαθηματικούς του μεγέθους του Euler, απαγορεύεται σήμερα δια ροπάλου.
, και τότε φυσικά δεν υπάρχει κανένα παράδοξο. Όμως το δίτιμο σύμβολο της τετραγωνικής ρίζας, που ήταν απολύτως νόμιμο και σεβαστό επί αιώνες και χρησιμοποιήθηκε με δεξιοτεχνία από μαθηματικούς του μεγέθους του Euler, απαγορεύεται σήμερα δια ροπάλου.Είναι προφανές ότι η δύναμη
 ορίζεται και είναι ίση με
ορίζεται και είναι ίση με  , μπορεί να μας το επιβεβαιώσουν, οι περισσότεροι μαθητές και των Ελληνικών Γυμνασίων, αφού το
, μπορεί να μας το επιβεβαιώσουν, οι περισσότεροι μαθητές και των Ελληνικών Γυμνασίων, αφού το  είναι ακέραιος. Αν το πάμε λίγο παραπέρα, τα διάφορα προβλήματα με το θέμα προκύπτουν από την κακή επιλογή του ορισμού της δύναμης με ρητό εκθέτη στο σχολικό βιβλίο της Α' Λυκείου. Διορθώνονται με δυο απλά βήματα. Δεχόμαστε στους πραγματικούς το φυσιολογικό, κάθε πραγματικός έχει μία κυβική ρίζα, άρα γράφω
είναι ακέραιος. Αν το πάμε λίγο παραπέρα, τα διάφορα προβλήματα με το θέμα προκύπτουν από την κακή επιλογή του ορισμού της δύναμης με ρητό εκθέτη στο σχολικό βιβλίο της Α' Λυκείου. Διορθώνονται με δυο απλά βήματα. Δεχόμαστε στους πραγματικούς το φυσιολογικό, κάθε πραγματικός έχει μία κυβική ρίζα, άρα γράφω ![\sqrt[3]{-8}=-2 \sqrt[3]{-8}=-2](/forum/ext/geomar/texintegr/latexrender/pictures/9dabfbb0c791ed02625a38b6a5934f93.png) , και κάθε θετικός πραγματικός αφού έχει δύο τετραγωνικές ρίζες με το σύμβολο
, και κάθε θετικός πραγματικός αφού έχει δύο τετραγωνικές ρίζες με το σύμβολο  να χρησιμοποιώ τη θετική άρα γράφω
να χρησιμοποιώ τη θετική άρα γράφω  , ενώ την αρνητική
, ενώ την αρνητική  . Έτσι όταν θα περάσουμε σε ρητό εκθέτη δεν θα ορίζονται μόνο εκείνες οι δυνάμεις με αρνητική βάση που έχουν εκθέτη ανάγωγο κλάσμα που οδηγεί σε άρτιας τάξης ριζικά. Οι ιδιότητες των δυνάμεων εξακολουθούν να ισχύουν. Αν ήταν έτσι τα πράγματα, όπως απέδειξε το αποτυχημένο εκ του αποτελέσματος θέμα του 2017 με την παράγωγο κυβικής ρίζας, τόσοι πολλοί υποψήφιοι δεν θα το αντιμετώπιζαν λάθος αφού τους ζητάμε να κατανοήσουν τα ακατανόητα. Η παρακάτω εικόνα είναι κατατοπιστική.
. Έτσι όταν θα περάσουμε σε ρητό εκθέτη δεν θα ορίζονται μόνο εκείνες οι δυνάμεις με αρνητική βάση που έχουν εκθέτη ανάγωγο κλάσμα που οδηγεί σε άρτιας τάξης ριζικά. Οι ιδιότητες των δυνάμεων εξακολουθούν να ισχύουν. Αν ήταν έτσι τα πράγματα, όπως απέδειξε το αποτυχημένο εκ του αποτελέσματος θέμα του 2017 με την παράγωγο κυβικής ρίζας, τόσοι πολλοί υποψήφιοι δεν θα το αντιμετώπιζαν λάθος αφού τους ζητάμε να κατανοήσουν τα ακατανόητα. Η παρακάτω εικόνα είναι κατατοπιστική.![\noindent\makebox[\linewidth]{\rule{\paperwidth}{0.07pt}} \noindent\makebox[\linewidth]{\rule{\paperwidth}{0.07pt}}](/forum/ext/geomar/texintegr/latexrender/pictures/d914bff1d8c2bd544e0a07967738e7a5.png)
 και
και 
 και
και  .
.


 δεχόμαστε ότι
δεχόμαστε ότι ![[\left ( -2 \right )^{6}]^{1/2}=[\left ( -2 \right )^{1/2}]^{6} [\left ( -2 \right )^{6}]^{1/2}=[\left ( -2 \right )^{1/2}]^{6}](/forum/ext/geomar/texintegr/latexrender/pictures/32a3c492ddac11a6e97939b5cecf99b4.png) το οποίο είναι εσφαλμένο καθώς το δεξί μέλος της τελευταίας ισότητας δεν είναι καλά ορισμένο.
το οποίο είναι εσφαλμένο καθώς το δεξί μέλος της τελευταίας ισότητας δεν είναι καλά ορισμένο. η δύναμη
η δύναμη  ορίζεται αν και μόνο αν
ορίζεται αν και μόνο αν 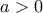 , ενώ η δύναμη
, ενώ η δύναμη  ορίζεται αν και μόνο αν
ορίζεται αν και μόνο αν  και
και  .
. είναι το
είναι το 
 δεν μπορούμε να γράψουμε.
δεν μπορούμε να γράψουμε. , η οποία ισχύει για
, η οποία ισχύει για  . Εδώ βέβαια έχουμε τη βάση -2 η οποία δεν είναι θετική, άρα δεν μπορούμε να την εφαρμόσουμε.
. Εδώ βέβαια έχουμε τη βάση -2 η οποία δεν είναι θετική, άρα δεν μπορούμε να την εφαρμόσουμε. (α)
(α)
 πληκτρολογείται σαν
πληκτρολογείται σαν  (σωστό) ή σαν
(σωστό) ή σαν  (λάθος). Στο τελευταίο το μηχανάκι εκτελεί
(λάθος). Στο τελευταίο το μηχανάκι εκτελεί  , διότι δεν "καταλαβαίνει" ότι το 2 αφορά τον εκθέτη (οπότε6/2=3).
, διότι δεν "καταλαβαίνει" ότι το 2 αφορά τον εκθέτη (οπότε6/2=3).  .
. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης