Έχει κάποιος συνάδελφος υπόψιν του που μπορώ να βρω την απόδειξη της πρότασης : "Το σύνολο
 εφοδιασμένο με τις πράξεις πρόσθεση και πολλαπλασιασμός modulo
εφοδιασμένο με τις πράξεις πρόσθεση και πολλαπλασιασμός modulo  είναι σώμα μόνο αν το
είναι σώμα μόνο αν το  είναι πρώτος αριθμός;"
είναι πρώτος αριθμός;"Ευχαριστώ.
Συντονιστής: nsmavrogiannis
 εφοδιασμένο με τις πράξεις πρόσθεση και πολλαπλασιασμός modulo
εφοδιασμένο με τις πράξεις πρόσθεση και πολλαπλασιασμός modulo  είναι σώμα μόνο αν το
είναι σώμα μόνο αν το  είναι πρώτος αριθμός;"
είναι πρώτος αριθμός;"Η απόδειξη δεν είναι δύσκολη και μπορεί να γίνει με πολλούς τρόπους. Ένας από αυτούς είναι στο proofwiki/Ring_of_Integers_Modulo_Prime_is_Field
 αποτελούν (πολλαπλασιαστική) ομάδα
αποτελούν (πολλαπλασιαστική) ομάδα  (ποια είναι αυτά;)
(ποια είναι αυτά;) είναι ακεραία περιοχή, τότε-τότε αν ο
είναι ακεραία περιοχή, τότε-τότε αν ο  είναι πρώτος.
είναι πρώτος.
 και όχι
και όχι  .
. το παραπάνω σύνολο είναι μεταθετικός δακτύλιος με
το παραπάνω σύνολο είναι μεταθετικός δακτύλιος με . Αν
. Αν  πρώτος, τότε είναι σώμα. Πράγματι, έστω
πρώτος, τότε είναι σώμα. Πράγματι, έστω  .
. είναι υποομάδα της
είναι υποομάδα της 
 , και τότε
, και τότε , που σημαίνει ότι το
, που σημαίνει ότι το  είναι
είναι είναι σώμα. Αν ο
είναι σώμα. Αν ο  δεν είναι πρώτος, τότε υπάρχει πρώτος διαιρέτης
δεν είναι πρώτος, τότε υπάρχει πρώτος διαιρέτης του
του  και γράφουμε
και γράφουμε  , όπου
, όπου  .
.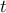 στην αβελιανή ομάδα
στην αβελιανή ομάδα  τάξης
τάξης  έχει
έχει , οπότε το ιδεώδες
, οπότε το ιδεώδες 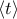 είναι μη τετριμμένο. Στα σώματα, τα
είναι μη τετριμμένο. Στα σώματα, τα και τότε
και τότε , όπως θέλαμε. Με την παραπάνω απόδειξη, αποδεικνύονται και όλα τα ερωτήματα που έθεσε ο Γρηγόρης.
, όπως θέλαμε. Με την παραπάνω απόδειξη, αποδεικνύονται και όλα τα ερωτήματα που έθεσε ο Γρηγόρης. είναι μεταθετικός δακτύλιος με μοναδιαίο.
είναι μεταθετικός δακτύλιος με μοναδιαίο. όχι πρώτος. Τότε
όχι πρώτος. Τότε 

 έχει μηδενοδιαιρέτες.Αρα το
έχει μηδενοδιαιρέτες.Αρα το  όχι σώμα.
όχι σώμα. είναι σώμα τότε ο
είναι σώμα τότε ο  είναι πρώτος.
είναι πρώτος. είναι πρώτος.
είναι πρώτος. τότε
τότε 

 είναι
είναι 
 υπάρχουν ακέραιοι με
υπάρχουν ακέραιοι με 
 κλπ
κλπΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες