Θα ήθελα οι λύσεις να γίνουν δίχως τη χρήση παραγώγων. (Εξηγήσεις θα ακολουθήσουν...)
Να βρεθεί το πεδίο τιμών του κλάσματος
 , όπου το
, όπου το  διατρέχει όλους τους πραγματικούς αριθμούς.
διατρέχει όλους τους πραγματικούς αριθμούς.Συντονιστής: nsmavrogiannis
 , όπου το
, όπου το  διατρέχει όλους τους πραγματικούς αριθμούς.
διατρέχει όλους τους πραγματικούς αριθμούς.ΚαλημέραΓιώργος Ρίζος έγραψε:Καλημέρα σε όλους.
Θα ήθελα οι λύσεις να γίνουν δίχως τη χρήση παραγώγων. (Εξηγήσεις θα ακολουθήσουν...)
Να βρεθεί το πεδίο τιμών του κλάσματος, όπου το
διατρέχει όλους τους πραγματικούς αριθμούς.


![\left[\dfrac{1}{3},3 \right], \left[\dfrac{1}{3},3 \right],](/forum/ext/geomar/texintegr/latexrender/pictures/12f68e63f57dd9224b7bd0ebb3a128db.png)
 . Όμως το σύνολο τιμών προκύπτει από την ένωση των διαστημάτων.....γνωστά
. Όμως το σύνολο τιμών προκύπτει από την ένωση των διαστημάτων.....γνωστά .
.STOPJOHN έγραψε:ΚαλημέραΓιώργος Ρίζος έγραψε:Καλημέρα σε όλους.
Θα ήθελα οι λύσεις να γίνουν δίχως τη χρήση παραγώγων. (Εξηγήσεις θα ακολουθήσουν...)
Να βρεθεί το πεδίο τιμών του κλάσματος, όπου το
διατρέχει όλους τους πραγματικούς αριθμούς.
Θέτουμε
Συνεπώς είναι
Το σύνολο τιμών του κλάσματος είναι το κλειστό διάστημα
Υποψιάζομαι ότι η παγίδα είναι στο. Όμως το σύνολο τιμών προκύπτει από την ένωση των διαστημάτων.....γνωστά
Φιλικά Γιάννης
Η οποία που ακριβώς διδάσκεται στα σχολικά βιβλία ;;;achilleas έγραψε:Καλησπέρα, Γιάννη,
Ευχαριστώ ιδιαίτερα για αυτή τη λύση!
Άλλο ένα παράδειγμα όπου η χρήση της διακρίνουσας είναι απολύτως σωστή στη συγκεκριμένη λύση, αν και οι συντελεστές εξαρτώνται από το.
Αχιλλέας
Λίγη υπομονή φίλτατε και θα απαντηθεί το ερώτημά σας. Απλά λίγη υπομονή.Atemlos έγραψε: Η οποία που ακριβώς διδάσκεται στα σχολικά βιβλία ;;;
 :
:
 :
: (ισότητα για
(ισότητα για  )
) για κάθε
για κάθε  (ισότητα για
(ισότητα για  )
) :
: και τελικά
και τελικά 
 για κάθε
για κάθε  (ισότητα για
(ισότητα για 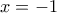 )
)
![[\frac{1}{3},3] [\frac{1}{3},3]](/forum/ext/geomar/texintegr/latexrender/pictures/e0a68cf61f07c7447270f47c1de9607e.png)
 για κάθε
για κάθε  ,
, ,
,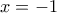 , ενώ
, ενώ
 .
.Όχι ακριβώς. Και με τους δυο τρόπους αποδεικνύουμε ότι το σύνολο τιμών περιέχεται στοB.Wolf έγραψε:....
άρα το σύνολο τιμών είναι το
![[\frac{1}{3},3] [\frac{1}{3},3]](/forum/ext/geomar/texintegr/latexrender/pictures/e0a68cf61f07c7447270f47c1de9607e.png) .
. Μπορούμε να αποφύγουμε τη συνέχεια υποθέτοντας οτι υπάρχειachilleas έγραψε: ...
Όχι ακριβώς. Και με τους δυο τρόπους αποδεικνύουμε ότι το σύνολο τιμών περιέχεται στοB.Wolf έγραψε:....
άρα το σύνολο τιμών είναι το.
Για την ισότητα χρειαζόμαστε είτε τη συνέχεια είτε τη δευτεροβάθμια εξίσωση, όμως.
Φιλικά,
Αχιλλέας
![\displaystyle{y\in [\frac{1}{3},3] \displaystyle{y\in [\frac{1}{3},3]](/forum/ext/geomar/texintegr/latexrender/pictures/a0d8a6f620e0922a0cec38b4ff7cd57b.png)
 για κάθε
για κάθε 
 καταλήγουμε σε άτοπο .
καταλήγουμε σε άτοπο . ειναι ανεξάρτητο του
ειναι ανεξάρτητο του  .
.Η συνέχεια αναφέρθηκε ως μια από τις επιλογές,makisman έγραψε:....
Μπορούμε να αποφύγουμε τη συνέχεια ...
όχι η μοναδική, και φυσικά αναφέρθηκε η 2θμια εξίσωση.achilleas έγραψε: ...
Για την ισότητα χρειαζόμαστε είτε τη συνέχεια είτε τη δευτεροβάθμια εξίσωση, όμως.
...
Επίσης, όταν μπορούμε να έχουμε μια απλή ευθεία απόδειξη, αποφεύγουμε την απαγωγή σε άτοπο.makisman έγραψε:.......
υποθέτοντας οτι υπάρχει
ώστεγια κάθε

και λύνοντας τη σχέση ως προςκαταλήγουμε σε άτοπο .
Φυσικά πάλι λύνουμε δευτεροβάθμια ,αλλά αυτή τη φορά τοειναι ανεξάρτητο του
.
![a\in [1/3,3] a\in [1/3,3]](/forum/ext/geomar/texintegr/latexrender/pictures/2755fba12828db5a2f21b9103f90df23.png) , τότε υπάρχει
, τότε υπάρχει  ώστε
ώστε  , λύνοντας μια εξίσωση 1ου βαθμού αν
, λύνοντας μια εξίσωση 1ου βαθμού αν  , και 2ου βαθμου με διακρίνουσα
, και 2ου βαθμου με διακρίνουσα  , αλλιώς.
, αλλιώς.Δεν υπάρχει απολύτως κανένα πρόβλημα με τη μέθοδο αυτή, στη λύση του Γιάννη, δηλαδή, που είναι πλήρης και διεθνώς "standard", αποδεκτή, ενώ είμαι σίγουρος ότι υπάρχει σε αμέτρητες αξιόλογες ελληνικές πηγές, επίσης.makisman έγραψε:Σωστά, το θέμα το ανέφερα πιο πολύ γιατί έτσι αποφεύγεται το περιβόητο πρόβλημα της εξάρτησης του y στη δευτεροβάθμια
Αχιλλέα ,εννοείται οτι δεν αντιδικώ με εσένα και εννοείται ότι αποδέχομαι πλήρως και τη λύση του Γιάννη. Το πρόβλημα δε το δημιουργώ εγώ ,που ούτε καν διορθωτής είμαι και το πρόβλημα δεν μπορεί να λυθεί μέσα από ένα νήμα συζήτησης .Απο τη στιγμή που δεν υπάρχει επίσημη Ελληνική θέση αν είναι αποδεκτή μια τέτοια λύση και από τη στιγμή που το θέμα επανέρχεται κάθε χρόνο σχεδόν ,εγώ τι να κάνω ; να το βάλω το χέρι μου στη φωτιά ; Όπως είπε και ο κ.Στεργίου σε άλλο θέμα πρέπει να γίνουν κάποιες κινήσεις ώστε να λυθούν αυτά τα ζητήματα ,αλλά μέχρι τότε ;achilleas έγραψε:Δεν υπάρχει απολύτως κανένα πρόβλημα με τη μέθοδο αυτή, στη λύση του Γιάννη, δηλαδή, που είναι πλήρης και διεθνώς "standard", αποδεκτή, ενώ είμαι σίγουρος ότι υπάρχει σε αμέτρητες αξιόλογες ελληνικές πηγές, επίσης.makisman έγραψε:Σωστά, το θέμα το ανέφερα πιο πολύ γιατί έτσι αποφεύγεται το περιβόητο πρόβλημα της εξάρτησης του y στη δευτεροβάθμια
Το θέμα αυτό το ανακαλύψανε ως "πρόβλημα" κάποιοι στην Ελλάδα. Ας μου παρουσιάσει κάποιος κάποιο άρθρο από ξενόγλωσσο περιοδικό.
Αφού είναι μείζονος σημασίας για τη μαθηματική ορθότητα, θα έπρεπε σίγουρα κάτι να έχει γραφτεί, σε κάποια γλώσσα.
Ρουμάνοι, Ρώσοι, Βούλγαροι, Ούγγροι, Βιετναμέζοι, Αμερικάνοι, και άλλοι, το αφήσανε να περάσει έτσι, και το ανακαλύψαμε εμείς;
Στην πραγματικότητα, είναι τόσο απλό που δε χρειάζεται καν ιδιαίτερη αναφορά σε οποιοδήποτε βιβλίο, σε οποιοδηποτε περιοδικό.
Η απάντηση είναι τόσο απλή!
Ποτέ δε μπορούσα να φανταστώ ότι θα αμφισβητούσαμε τα προφανή, μόνο και μόνο από σεβασμό σε κάποιον.
Η αλήθεια είναι αλήθεια! Ας τελειώσει πια αυτό το θέμα.
Φιλικά,
Αχιλλέας
Δε νομίζω να χειάζεται να διδαχθεί κάτι τέτοιο για να μπορεί να το χρησιμοποιήσει κανείς. Βέβαια καλό θα ήταν να υπήρχε ένα παράδειγμα ή εφαρμογή σε σχολικό βιβλίο ώστε ο μαθητής να έρθει σε επαφή με αυτή την μέθοδο.Atemlos έγραψε: Η οποία που ακριβώς διδάσκεται στα σχολικά βιβλία ;;;
Σε εισαγωγικές εξετάσεις στη Ρωσία συχνά πέφτουν παρόμοια θέματα. Για παράδειγμα η άσκηση εδώ.axilleas έγραψε: Αφού είναι μείζονος σημασίας για τη μαθηματική ορθότητα, θα έπρεπε σίγουρα κάτι να έχει γραφτεί, σε κάποια γλώσσα.
Ρουμάνοι, Ρώσοι, Βούλγαροι, Ούγγροι, Βιετναμέζοι, Αμερικάνοι, και άλλοι, το αφήσανε να περάσει έτσι, και το ανακαλύψαμε εμείς;
Το σχόλιο αυτό αφορούσε τη χρήση της διακρίνουσας, και όχι το προτεινόμενο πρόβλημα του Γιώργου.Al.Koutsouridis έγραψε:...Σε εισαγωγικές εξετάσεις στη Ρωσία συχνά πέφτουν παρόμοια θέματα. Για παράδειγμα η άσκηση εδώ.axilleas έγραψε: Αφού είναι μείζονος σημασίας για τη μαθηματική ορθότητα, θα έπρεπε σίγουρα κάτι να έχει γραφτεί, σε κάποια γλώσσα.
Ρουμάνοι, Ρώσοι, Βούλγαροι, Ούγγροι, Βιετναμέζοι, Αμερικάνοι, και άλλοι, το αφήσανε να περάσει έτσι, και το ανακαλύψαμε εμείς;
 , με
, με  για
για  . Τί πραγματικές τιμές παίρνει το κλάσμα
. Τί πραγματικές τιμές παίρνει το κλάσμα 
 για
για  . Έτσι, η
. Έτσι, η  είναι η διακρίνουσα του αριθμητή και η
είναι η διακρίνουσα του αριθμητή και η  η διακρίνουσα του παρονομαστή, αλλα έχουμε και δύο μπασταρδεμένες.
η διακρίνουσα του παρονομαστή, αλλα έχουμε και δύο μπασταρδεμένες. το σύνολο τιμών του κλάσματος, το οποίο καλούμαστε να προσδιορίσουμε. Ένα οποιοδήποτε
το σύνολο τιμών του κλάσματος, το οποίο καλούμαστε να προσδιορίσουμε. Ένα οποιοδήποτε  θ' ανήκει εξορισμού στο
θ' ανήκει εξορισμού στο  , άν ικανοποιεί τη φόρμουλα
, άν ικανοποιεί τη φόρμουλα
 (το «φιξάρουμε» που λέμε) --ανεξάρτητα απο το
(το «φιξάρουμε» που λέμε) --ανεξάρτητα απο το  , άς το τονίσω αυτό εδώ-- και θέλουμε να καταλάβουμε καλύτερα τί πρέπει να ικανοποιεί προκειμένου ν' ανήκει στο
, άς το τονίσω αυτό εδώ-- και θέλουμε να καταλάβουμε καλύτερα τί πρέπει να ικανοποιεί προκειμένου ν' ανήκει στο  . Ήδη πρέπει να πούμε οτι άν ο παρονομαστής είναι μηδέν, τότε το σύνολο που ψάχνουμε είναι κενό: το κλάσμα δέν παίρνει πραγματικές τιμές, δέν ορίζεται. (Άν είναι να δούμε συνεπώς το κλάσμα ώς συνάρτηση, και δή ολική συνάρτηση, θα πρέπει να την ορίσουμε το πολύ στο
. Ήδη πρέπει να πούμε οτι άν ο παρονομαστής είναι μηδέν, τότε το σύνολο που ψάχνουμε είναι κενό: το κλάσμα δέν παίρνει πραγματικές τιμές, δέν ορίζεται. (Άν είναι να δούμε συνεπώς το κλάσμα ώς συνάρτηση, και δή ολική συνάρτηση, θα πρέπει να την ορίσουμε το πολύ στο  · όχι οτι χρειάζεται να το δούμε ώς συνάρτηση βέβαια.)
· όχι οτι χρειάζεται να το δούμε ώς συνάρτηση βέβαια.) είναι ισοδύναμη με την φόρμουλα
είναι ισοδύναμη με την φόρμουλα
 , και τότε έχουμε ήδη μία πιθανή αποδεκτή μορφή για το
, και τότε έχουμε ήδη μία πιθανή αποδεκτή μορφή για το  , δηλαδή την τιμή
, δηλαδή την τιμή  . Λέω «πιθανή» όμως. Γιατι για ποιό όρισμα την παίρνουμε αυτήν; Υπόψιν οτι το ερώτημα «για ποιό όρισμα» δέν προκύπτει απο κάποιου είδους μαθηματικό μαζοχισμό, αλλα το θέτει αυτόματα ο ποσοδείκτης!: αυτός ειναι που απαιτεί να εντοπίσουμε ένα (τουλάχιστον)
. Λέω «πιθανή» όμως. Γιατι για ποιό όρισμα την παίρνουμε αυτήν; Υπόψιν οτι το ερώτημα «για ποιό όρισμα» δέν προκύπτει απο κάποιου είδους μαθηματικό μαζοχισμό, αλλα το θέτει αυτόματα ο ποσοδείκτης!: αυτός ειναι που απαιτεί να εντοπίσουμε ένα (τουλάχιστον)  για το οποίο το κλάσμα να παίρνει την συγκεκριμένη τιμή, αλλιώς η απόδειξη θα είναι λειψή.
για το οποίο το κλάσμα να παίρνει την συγκεκριμένη τιμή, αλλιώς η απόδειξη θα είναι λειψή. όπου
όπου  το
το  , και κάνοντας ανώδυνες πράξεις, φτάνουμε στην ισοδύναμη φόρμουλα
, και κάνοντας ανώδυνες πράξεις, φτάνουμε στην ισοδύναμη φόρμουλα
 ικανοποιείται ακριβώς όταν
ικανοποιείται ακριβώς όταν
 να επιλέξουμε όποιο συγκεκριμένο
να επιλέξουμε όποιο συγκεκριμένο  τραβά η όρεξή μας (έντιτ: άν ισχύει το δεξιό διάζευγμα! άν ισχύει το αριστερό, παίρνουμε βέβαια το μοναδικό
τραβά η όρεξή μας (έντιτ: άν ισχύει το δεξιό διάζευγμα! άν ισχύει το αριστερό, παίρνουμε βέβαια το μοναδικό  --σόρι). Απ' την άλλη, ο ποσοδείκτης δέν περιττεύει καθόλου στη φόρμουλα
--σόρι). Απ' την άλλη, ο ποσοδείκτης δέν περιττεύει καθόλου στη φόρμουλα  : άμα έχουμε
: άμα έχουμε  αλλα
αλλα  , η
, η  δέν ικανοποιείται (δέν υπάρχουν τέτοια
δέν ικανοποιείται (δέν υπάρχουν τέτοια  ) και άρα η
) και άρα η  δέν είναι αποδεκτή ως τιμή του κλάσματος!
δέν είναι αποδεκτή ως τιμή του κλάσματος! , υποθέτοντας αυτήν τη φορά οτι
, υποθέτοντας αυτήν τη φορά οτι  . Τί μας λέει η φόρμουλα σ' αυτήν την περίπτωση; οτι το
. Τί μας λέει η φόρμουλα σ' αυτήν την περίπτωση; οτι το  για το οποίο συζητάμε είναι τιμή του κλάσματος άν και μόνο άν το τριώνυμο
για το οποίο συζητάμε είναι τιμή του κλάσματος άν και μόνο άν το τριώνυμο  έχει πραγματικές ρίζες. Μ' άλλα λόγια, το
έχει πραγματικές ρίζες. Μ' άλλα λόγια, το  είναι όπως το θέλουμε άν και μόνο άν η διακρίνουσα
είναι όπως το θέλουμε άν και μόνο άν η διακρίνουσα  του
του  είναι μή αρνητική. Η διακρίνουσα αυτή, με απλές αλλα προσεκτικές πράξεις, βγαίνει ίση με την παράσταση
είναι μή αρνητική. Η διακρίνουσα αυτή, με απλές αλλα προσεκτικές πράξεις, βγαίνει ίση με την παράσταση  , άρα τελικά η
, άρα τελικά η  γράφεται ισοδύναμα
γράφεται ισοδύναμα
 , στο οποίο πλέον καλούμαστε να κάνουμε μελέτη προσήμου: τα
, στο οποίο πλέον καλούμαστε να κάνουμε μελέτη προσήμου: τα  που θέλουμε, είναι ακριβώς εκείνα για τα οποία το
που θέλουμε, είναι ακριβώς εκείνα για τα οποία το  είναι μή αρνητικό, και για να τα εντοπίσουμε θα πρέπει να εξετάσουμε τη διακρίνουσα
είναι μή αρνητικό, και για να τα εντοπίσουμε θα πρέπει να εξετάσουμε τη διακρίνουσα  κατα τα γνωστά. Και προσέξτε πάλι το εξής: στην τελευταία φόρμουλα δέ χρειαζόμαστε ποσόδειξη του
κατα τα γνωστά. Και προσέξτε πάλι το εξής: στην τελευταία φόρμουλα δέ χρειαζόμαστε ποσόδειξη του  : όλα εκείνα τα
: όλα εκείνα τα  εξαρτιούνται μόνο απ' τα
εξαρτιούνται μόνο απ' τα  (και το
(και το  φυσικά έχει φιξαριστεί ανεξάρτητα απ' το
φυσικά έχει φιξαριστεί ανεξάρτητα απ' το  ήδη απ' την αρχή).
ήδη απ' την αρχή). απο αριθμητή και παρονομαστή του αρχικού κλάσματος, ένα τριώνυμο
απο αριθμητή και παρονομαστή του αρχικού κλάσματος, ένα τριώνυμο  του
του  στη
στη  και άλλο ένα τριώνυμο
και άλλο ένα τριώνυμο  , αυτήν τη φορά του
, αυτήν τη φορά του  , στη φόρμουλα
, στη φόρμουλα  . Να τ' αφήσω;...
. Να τ' αφήσω;... είναι λάθος, η σωστή είναι
είναι λάθος, η σωστή είναι
Απολαμβάνω να διαβάζω τα κείμενα του Σίλη. Το κακό είναι ότι παρασύρομαι από το γλαφυρό λόγο κι ενίοται χάνομαι (γιατί ρεμβάζω).Σίλης έγραψε: Πέρ' απ' αυτά τα παραμαθηματικά, θα είχε ενδιαφέρον να σκαρφιστεί κανείς ύπουλες ασκήσεις με βάση τη γενική μορφή του κλάσματος (αυτή ηταν η ιδέα μου αρχικά, αλλα στο μεταξύ τα έγραψα ήδη πολλά...). Υπάρχουνε πολλά ουσιωδώς διαφορετικά κλάσματα τριωνύμων που να προσφέρονται για σχολικές ασκήσεις τέτοιου τύπου, ή ουσιαστικά το κλάσμα του αρχικού πόστ ήδη καλύπτει ότι κρίνεται άξιο να διδαχτεί στην τάξη;... Δέ ξέρω.
Έντιτ: Και αλήθεια, τί θα λέγατε στα παιδιά οτι τους διδάσκει αυτή η άσκηση ακριβώς; (εννοώ του αρχικού πόστ)
Αν, όχι, να ψάξω και σε άλλα παλαιότερα σχολικά βιβλία, που τουλάχιστον εγώ τα διδάχτηκα ως μαθητής.Atemlos έγραψε:Η οποία που ακριβώς διδάσκεται στα σχολικά βιβλία ;;;achilleas έγραψε:Καλησπέρα, Γιάννη,
Ευχαριστώ ιδιαίτερα για αυτή τη λύση!
Άλλο ένα παράδειγμα όπου η χρήση της διακρίνουσας είναι απολύτως σωστή στη συγκεκριμένη λύση, αν και οι συντελεστές εξαρτώνται από το.
Αχιλλέας
 , όταν ο τύπος της είναι
, όταν ο τύπος της είναι 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες