socrates έγραψε:Άσκηση 16
Οι παίκτες Α και Β ρίχνουν διαδοχικά δύο συνηθισµένα ζάρια, µέχρις ότου είτε ο Α φέρει πρώτος άθροισµα 9, οπότε το παιχνίδι το κερδίζει ο Α, ή ο Β φέρει πρώτος
άθροισµα 8, οπότε το παιχνίδι το κερδίζει ο Β. Οι ρίψεις ξεκινούν από τον Α. Να υπολογίσετε την πιθανότητα να κερδίσει ο Α, καθώς και την πιθανότητα να κερδίσει ο Β.
Είναι σωστό να ισχυριστούμε ότι το παιχνίδι θα τελειώσει σε πεπερασμένο πλήθος ρίψεων;
Η πιθανότητα να φέρει ο

άθροισμα

στην ζαριά του είναι


, τέσσερα ευνοικά ενδεχόμενα στα

και η πιθανότητα να μην φέρει άθροισμα

είναι

Η πιθανότητα να φέρει ο

άθροισμα

στην ζαριά του είναι


, πέντε ευνοικά ενδεχόμενα στα

) και η πιθανότητα να μην φέρει άθροισμα

είναι

.
Άρα




και


Δεν θεωρώ σωστό
να ισχυρισθούμε ότι το παιχνίδι θα τελειώσει σε πεπερασμένο πλήθος ρίψεων, γιατί το παιχνίδι μπορεί να παρατείνεται επ' αόριστον με όλο και ελαχιστότερη πιθανότητα βέβαια, καθώς

και

πρoέκυψαν ως όρια ακολουθιών (ή κάπως έτσι διατυπωμένο). Το
πιο πιθανό βέβαια είναι να λήξει σε πεπερασμένο πλήθος ρίψεων.
Προσθέτω αναλυτικό και επεξηγηματικό, για νεότερους που δεν είναι εξοικειωμένοι και παρά το κουραστικό της
latex γραφής, υπολογισμό της πιθανότητας

να κερδίσει ο

αν και ήδη μας είναι γνωστή αφού έχοντας υπολογίσει την πιθανότητα

να κερδίσει ο

καθώς το άθροισμα των οριακών

και

είναι:

Η πιθανότητα να κερδίσει ο

είναι το άθροισμα των επιμέρους πιθανοτήτων σε κάθε ρίψη των δύο ζαριών.
Έτσι στην

η ρίψη του

στον πρώτο “γύρο” για να κερδίσει πρέπει να έχει χάσει ο

(να μην φέρει άθροισμα

), πιθανότητα να συμβεί αυτό είναι

και ο ίδιος να φέρει άθροισμα

, με πιθανότητα

, άρα πιθανότητα

.
Για να κερδίσει στην

η ρίψη του πρέπει να έχουν χάσει και οι δύο στις πρώτες ρίψεις τους και ο

να χάσει και στην δεύτερη ρίψη του και ο ίδιος να φέρει άθροισμα

στην δεύτερη ρίψη του, άρα πιθανότητα να συμβεί αυτό είναι

.
Στον

ο γύρο πρέπει να έχουν χάσει και οι δύο στους δύο πρώτους γύρους, πιθανότητα να συμβεί αυτό

και στον

ο γύρο ο

να χάσει και ο

να κερδίσει, άρα πιθανότητα να συμβεί αυτό

κ.ο.κ ...
Άρα η συνολική πιθανότητα να κερδίσει ο

είναι




σχηματίζουμε τριψήφιους φυσικούς αριθμούς χωρίς επανάληψη ψηφίου. Να βρείτε:
 τριψήφιοι αριθμοί
τριψήφιοι αριθμοί φορές αντίστοιχα, άρα το άθροισμα όλων των αριθμών είναι:
φορές αντίστοιχα, άρα το άθροισμα όλων των αριθμών είναι: 

 αναγραμματισμούς.
αναγραμματισμούς. .
.  αναγραμματισμούς.
αναγραμματισμούς.
 και
και 
 άθροισμα
άθροισμα  στην ζαριά του είναι
στην ζαριά του είναι 
 , τέσσερα ευνοικά ενδεχόμενα στα
, τέσσερα ευνοικά ενδεχόμενα στα  και η πιθανότητα να μην φέρει άθροισμα
και η πιθανότητα να μην φέρει άθροισμα 
 άθροισμα
άθροισμα  στην ζαριά του είναι
στην ζαριά του είναι 
 , πέντε ευνοικά ενδεχόμενα στα
, πέντε ευνοικά ενδεχόμενα στα  ) και η πιθανότητα να μην φέρει άθροισμα
) και η πιθανότητα να μην φέρει άθροισμα  .
.


 και
και 

 και
και  πρoέκυψαν ως όρια ακολουθιών (ή κάπως έτσι διατυπωμένο). Το
πρoέκυψαν ως όρια ακολουθιών (ή κάπως έτσι διατυπωμένο). Το
 η ρίψη του
η ρίψη του  και ο ίδιος να φέρει άθροισμα
και ο ίδιος να φέρει άθροισμα  , άρα πιθανότητα
, άρα πιθανότητα  .
.  η ρίψη του πρέπει να έχουν χάσει και οι δύο στις πρώτες ρίψεις τους και ο
η ρίψη του πρέπει να έχουν χάσει και οι δύο στις πρώτες ρίψεις τους και ο  .
. ο γύρο πρέπει να έχουν χάσει και οι δύο στους δύο πρώτους γύρους, πιθανότητα να συμβεί αυτό
ο γύρο πρέπει να έχουν χάσει και οι δύο στους δύο πρώτους γύρους, πιθανότητα να συμβεί αυτό  και στον
και στον  κ.ο.κ ...
κ.ο.κ ...



 του παραπάνω πίνακα( στην εικόνα) περιγράφουν την πιθανότητα μεταξύ αυτών των ατόμων τα πέντε να είναι αριστερόχειρα.
του παραπάνω πίνακα( στην εικόνα) περιγράφουν την πιθανότητα μεταξύ αυτών των ατόμων τα πέντε να είναι αριστερόχειρα. και η
και η 
 διαιρούνται
διαιρούνται  αριθμοί
αριθμοί διαιρούνται
διαιρούνται  αριθμοί
αριθμοί διαιρούνται
διαιρούνται  αριθμοί
αριθμοί . Το πλήθος αριθμών που διαιρούνται με το
. Το πλήθος αριθμών που διαιρούνται με το  είναι
είναι 
 . Άρα
. Άρα  αριθμοί
αριθμοί . Άρα
. Άρα  . Άρα
. Άρα  , που διαιρούνται τουλάχιστον με έναν από του
, που διαιρούνται τουλάχιστον με έναν από του 

 , είναι το
, είναι το  είναι επίσης το
είναι επίσης το 
 η πιθανότητα να κερδίσει ο
η πιθανότητα να κερδίσει ο  Αυτό ισχύει επειδή η πιθανότητα να κερδίσει ο
Αυτό ισχύει επειδή η πιθανότητα να κερδίσει ο  .
. να μην τελειώσει το παιγνίδι μετά από
να μην τελειώσει το παιγνίδι μετά από  γύρους είναι
γύρους είναι  αν
αν 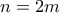 και
και  αν
αν  . Επειδή
. Επειδή  (απλό) η πιθανότητα να υπάρξει νικητής ισούται με
(απλό) η πιθανότητα να υπάρξει νικητής ισούται με  η πιθανότητα να κερδίσει ο
η πιθανότητα να κερδίσει ο  .
.  και πάλι να καταλήξουμε στο
και πάλι να καταλήξουμε στο  .]
.]
 με
με  οι τυχαίοι αριθμοί των πέντε ζαριών. Θέλουμε να ισχύει
οι τυχαίοι αριθμοί των πέντε ζαριών. Θέλουμε να ισχύει 
 μείον το πλήθος των ακέραιων λύσεων της εξίσωσης
μείον το πλήθος των ακέραιων λύσεων της εξίσωσης 

 και το οποίο ισούται με:
και το οποίο ισούται με:

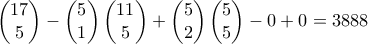
 ευνοικές περιπτώσεις για Ά(θροισμα)
ευνοικές περιπτώσεις για Ά(θροισμα)  και άρα η πιθανότητα είναι
και άρα η πιθανότητα είναι 
 αφαιρούμε από το πλήθος των
αφαιρούμε από το πλήθος των  ευνοικών περιπτώσεων ενδείξεων με
ευνοικών περιπτώσεων ενδείξεων με  το πλήθος των περιπτώσεων ενδείξεων με
το πλήθος των περιπτώσεων ενδείξεων με  και
και 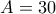 ,
,  περιπτώσεις, άρα
περιπτώσεις, άρα  .
.  (δυσανάλογης βαρύτητας ερώτημα σε σχέση με τα (α) και (γ) ή μήπως κάτι μου έχει διαφύγει?)
(δυσανάλογης βαρύτητας ερώτημα σε σχέση με τα (α) και (γ) ή μήπως κάτι μου έχει διαφύγει?)
 δυνατά αθροίσματα).
δυνατά αθροίσματα). έως και
έως και  , είναι τα μισά (
, είναι τα μισά ( αθροίσματα) και από
αθροίσματα) και από  έως και
έως και  συμπεραίνουμε ότι σε όσες περιπτώσεις έχουμε άθροισμα
συμπεραίνουμε ότι σε όσες περιπτώσεις έχουμε άθροισμα  σε ακριβώς τόσες έχουμε
σε ακριβώς τόσες έχουμε 
 περιπτώσεις και άρα
περιπτώσεις και άρα 


 ο συνολικός αριθμός των Γερμανών. Επειδή ο πληθυσμός είναι μεγάλος, η διαφορά στις απαντήσεις είναι τόσο μικρή που πρακτικά να μην κάνει διαφορά.
ο συνολικός αριθμός των Γερμανών. Επειδή ο πληθυσμός είναι μεγάλος, η διαφορά στις απαντήσεις είναι τόσο μικρή που πρακτικά να μην κάνει διαφορά. περιέχουν τον αριθμό που είναι ίσος με το πλήθος των στοιχείων του υποσυνόλου αυτού;
περιέχουν τον αριθμό που είναι ίσος με το πλήθος των στοιχείων του υποσυνόλου αυτού;  τα σφαιρίδια και
τα σφαιρίδια και 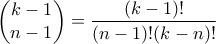
 καραμέλες και
καραμέλες και  ημέρες, καθώς μπορεί να τις φάει όλες σε μια ημέρα με
ημέρες, καθώς μπορεί να τις φάει όλες σε μια ημέρα με  τρόπο ή σε
τρόπο ή σε  τρόπους, ή σε
τρόπους, ή σε  τρόπους,...,ή σε
τρόπους,...,ή σε  τρόπο.
τρόπο. 


 τρόπους,
τρόπους, τρόπους (
τρόπους (  τρόπους
τρόπους
