Ένα διαγώνισμα αποτελείται από μία μόνο ερώτηση. Υπάρχουν
 πιθανές ερωτήσεις.
πιθανές ερωτήσεις. Ένας μαθητής γνωρίζει την απάντηση σε μόνο μια ερώτηση, αλλά μπορεί να κάνει το διαγώνισμα
 φορές.
φορές. Ποια η πιθανότητα,
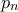 , ο μαθητής να περάσει το διαγώνισμα;
, ο μαθητής να περάσει το διαγώνισμα; Καθώς αυξάνει το
 , η πιθανότητα
, η πιθανότητα 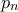 αυξάνεται ή μειώνεται;
αυξάνεται ή μειώνεται; Ποιο το όριο
 ; Ποιο το μέγιστο κάτω φράγμα των πιθανοτήτων
; Ποιο το μέγιστο κάτω φράγμα των πιθανοτήτων 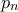 ;
;ΑΣΚΗΣΗ 9
Έχουμε δυο σακούλια με κόκκινους και μπλε βόλους, έναν τουλάχιστον από κάθε χρώμα σε κάθε σακούλι.
Υποθέτουμε ότι αν διαλέξουμε στην τύχη ένα από τα σακούλια και έπειτα έναν βόλο από αυτό, η πιθανότητα να είναι κόκκινος είναι ίση με την αντίστοιχη πιθανότητα αν βάλουμε όλους τους βόλους σε ένα σακούλι και διαλέξουμε ένα βόλο.
Αν το πρώτο σακούλι περιέχει 7 βόλους και το δεύτερο 5 κόκκινους βόλους, να βρείτε πόσους βόλους περιέχει συνολικά το δεύτερο σακούλι.

 τρόποι να επιλέξουμε τις θέσεις που θα εμφανιστούν εξάρια. Στις υπόλοιπες
τρόποι να επιλέξουμε τις θέσεις που θα εμφανιστούν εξάρια. Στις υπόλοιπες  θέσεις πρέπει να εμφανίζονται αριθμοί από το σύνολο
θέσεις πρέπει να εμφανίζονται αριθμοί από το σύνολο  . Οπότε υπάρχουν
. Οπότε υπάρχουν 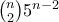 διαφορετικοί τρόποι να εμφανίζονται ακριβώς
διαφορετικοί τρόποι να εμφανίζονται ακριβώς  εξάρια. Επομένως η πιθανότητα είναι
εξάρια. Επομένως η πιθανότητα είναι 
 , χωρίς λογισμό, παρατηρούμε ότι
, χωρίς λογισμό, παρατηρούμε ότι 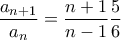 και άρα
και άρα  με ισότητα αν και μόνο αν
με ισότητα αν και μόνο αν  . Οπότε έχουμε
. Οπότε έχουμε  και
και  . Δηλαδή η πιθανότητα μεγιστοποιείται αν ρίξουμε είτε
. Δηλαδή η πιθανότητα μεγιστοποιείται αν ρίξουμε είτε  είτε
είτε  ζάρια.
ζάρια. σε κάθε επανάληψη, άρα έχουμε διωνυμική κατανομή, διακριτή συνάρτηση κατανομής τυχαίας μεταβλητής.
σε κάθε επανάληψη, άρα έχουμε διωνυμική κατανομή, διακριτή συνάρτηση κατανομής τυχαίας μεταβλητής. που εκφράζει τον αριθμό των επιτυχιών. Η πιθανότητα να έχουμε
που εκφράζει τον αριθμό των επιτυχιών. Η πιθανότητα να έχουμε  επιτυχίες σε
επιτυχίες σε 
 . Είναι
. Είναι  .
.  . Άρα όσο αυξάνει το
. Άρα όσο αυξάνει το  . To μέγιστο κάτω φράγμα είναι προφανώς το
. To μέγιστο κάτω φράγμα είναι προφανώς το  , μία η ερώτηση από μία συνολικά ερωτήσεις, μία γνωρίζει, επιτυχία.
, μία η ερώτηση από μία συνολικά ερωτήσεις, μία γνωρίζει, επιτυχία. 
 σακούλι περιέχει
σακούλι περιέχει  κόκκινους βόλους και το
κόκκινους βόλους και το  σακούλι
σακούλι  βόλους συνολικά.
βόλους συνολικά. , να επιλέξουμε ένα κόκκινο βόλο από ένα τυχαίο σακούλι είναι:
, να επιλέξουμε ένα κόκκινο βόλο από ένα τυχαίο σακούλι είναι: 

 , να επιλέξουμε έναν βόλο αφού τους βάλουμε όλους σε ένα σακούλι είναι:
, να επιλέξουμε έναν βόλο αφού τους βάλουμε όλους σε ένα σακούλι είναι: 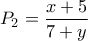 .
. 


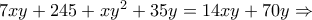
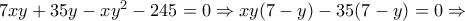

 ή
ή 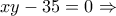
 , ή
, ή 
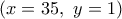 απορρίπτεται, όπως απορρίπτεται και η
απορρίπτεται, όπως απορρίπτεται και η 
 και
και 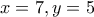 γίνεται γιατί αφού το
γίνεται γιατί αφού το  δεν μπορεί να έχει
δεν μπορεί να έχει  κόκκινους!, όπως δεν μπορεί να έχει
κόκκινους!, όπως δεν μπορεί να έχει  κόκκινους δεν μπορεί να έχει σύνολο
κόκκινους δεν μπορεί να έχει σύνολο 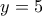 , δεν υπάρχει μπλέ. (από τα δεδομένα "έναν τουλάχιστον από κάθε χρώμα σε κάθε σακούλι")
, δεν υπάρχει μπλέ. (από τα δεδομένα "έναν τουλάχιστον από κάθε χρώμα σε κάθε σακούλι")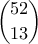 τρόπους. Ο δεύτερος με
τρόπους. Ο δεύτερος με  τρόπους, ο τρίτος με
τρόπους, ο τρίτος με  τρόπους και ο τέταρτος με
τρόπους και ο τέταρτος με  τρόπους.
τρόπους.  τρόπους να μοιράσουμε την τράπουλα στους 4 παίχτες.
τρόπους να μοιράσουμε την τράπουλα στους 4 παίχτες. 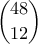 τρόπους. Ο δεύτερος με
τρόπους. Ο δεύτερος με  τρόπους, ο τρίτος με
τρόπους, ο τρίτος με  τρόπους και ο τέταρτος με
τρόπους και ο τέταρτος με 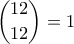 τρόπους. Για κάθε τέτοια μοιρασιά, μπορούμε να μοιράσουμε τους άσσους με
τρόπους. Για κάθε τέτοια μοιρασιά, μπορούμε να μοιράσουμε τους άσσους με 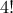 τρόπους.
τρόπους.  τρόπους να μοιράσουμε την τράπουλα στους 4 παίχτες, έτσι ώστε ο καθένας να έχει έναν ακριβώς άσσο.
τρόπους να μοιράσουμε την τράπουλα στους 4 παίχτες, έτσι ώστε ο καθένας να έχει έναν ακριβώς άσσο.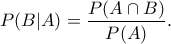
 είναι αυτή αυτή που υπολογίσαμε στο α). Μένει, λοιπόν, να βρούμε την πιθανότητα
είναι αυτή αυτή που υπολογίσαμε στο α). Μένει, λοιπόν, να βρούμε την πιθανότητα 
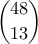 τρόπους να επιλέξω τα φύλλα μου και να μην έχω πάρει άσσο.
τρόπους να επιλέξω τα φύλλα μου και να μην έχω πάρει άσσο.  και
και 




 φύλλα που πήρε, τα τρία (
φύλλα που πήρε, τα τρία ( ) άλλα άτομα παίζουν με τράπουλα ...
) άλλα άτομα παίζουν με τράπουλα ...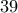 φύλλων με τρεις άσσους σε αυτά και πρέπει να πάρουν έναν άσσο ο καθένας, άρα η πιθανότητα να συμβεί αυτό είναι:
φύλλων με τρεις άσσους σε αυτά και πρέπει να πάρουν έναν άσσο ο καθένας, άρα η πιθανότητα να συμβεί αυτό είναι: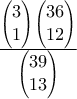
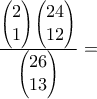
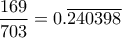
 ενώ
ενώ  είναι η πιθανότητα να το κερδίσει
είναι η πιθανότητα να το κερδίσει





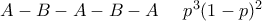

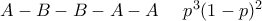

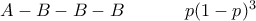




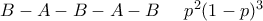
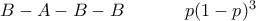

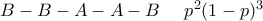
















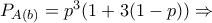




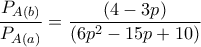

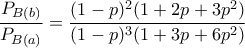


 να πάρει το κύπελλο η ομάδα
να πάρει το κύπελλο η ομάδα  να πάρει το κύπελλο η ομάδα
να πάρει το κύπελλο η ομάδα  .
. και
και  για
για 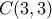 , με πιθανότητα να συμβεί αυτό
, με πιθανότητα να συμβεί αυτό 
 περιπτώσεις, από όπου πρέπει να αφαιρεθεί η περίπτωση
περιπτώσεις, από όπου πρέπει να αφαιρεθεί η περίπτωση 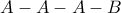

 περιπτώσεις, από όπου πρέπει να αφαιρεθούν τα
περιπτώσεις, από όπου πρέπει να αφαιρεθούν τα  . Η συνολική πιθανότητα να κερδίσει η
. Η συνολική πιθανότητα να κερδίσει η 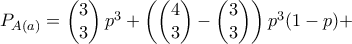

 και
και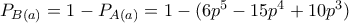

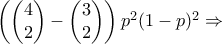

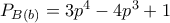 και
και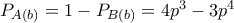
 αυτά παιδιά ;
αυτά παιδιά ; )
) τρόπους
τρόπους με
με 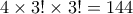 τρόπους. Τα αγόρια μπορούν να καθίσουν μαζί επίσης με
τρόπους. Τα αγόρια μπορούν να καθίσουν μαζί επίσης με 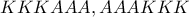 , ήτοι
, ήτοι 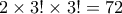 τρόποι. (Βλέπω ένα προβληματάκι στη διατύπωση όσον αφορά το “και”, η εγώ έχω προβληματάκι στο να αντιληφθώ την μαθηματική σημασία του “και”. Το αποτέλεσμα όμως,
τρόποι. (Βλέπω ένα προβληματάκι στη διατύπωση όσον αφορά το “και”, η εγώ έχω προβληματάκι στο να αντιληφθώ την μαθηματική σημασία του “και”. Το αποτέλεσμα όμως, 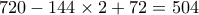 τρόπους.
τρόπους.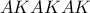 ή
ή 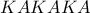 , ήτοι με
, ήτοι με  τρόπους.
τρόπους. τρόπους
τρόπους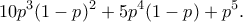
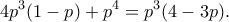
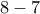 . Πως πρέπει να μοιράσουν τα 10 ευρώ του στοιχήματος ώστε να είναι δίκαιη η μοιρασιά;
. Πως πρέπει να μοιράσουν τα 10 ευρώ του στοιχήματος ώστε να είναι δίκαιη η μοιρασιά;
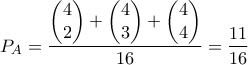 και ο Βασίλης
και ο Βασίλης 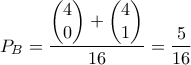
 ευρώ και ο Βασίλης
ευρώ και ο Βασίλης  ευρώ.
ευρώ.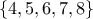 σχηματίζουμε τριψήφιους φυσικούς αριθμούς χωρίς επανάληψη ψηφίου. Να βρείτε:
σχηματίζουμε τριψήφιους φυσικούς αριθμούς χωρίς επανάληψη ψηφίου. Να βρείτε: