 αριθμός Γιώργου.
αριθμός Γιώργου. αριθμός Μαρίας.
αριθμός Μαρίας. συναρτήσεις πυκνότητας πιθανότητας των
συναρτήσεις πυκνότητας πιθανότητας των  και
και  , αντίστοιχα.
, αντίστοιχα.Η ζητούμενη πιθανότητα είναι


Συντονιστής: nsmavrogiannis
 αριθμός Γιώργου.
αριθμός Γιώργου. αριθμός Μαρίας.
αριθμός Μαρίας. συναρτήσεις πυκνότητας πιθανότητας των
συναρτήσεις πυκνότητας πιθανότητας των  και
και  , αντίστοιχα.
, αντίστοιχα.

 πρώτος και
πρώτος και  να αποδειχθεί ότι ο
να αποδειχθεί ότι ο  διαιρεί τον
διαιρεί τον 
Είναι
 άρα οι διαιρέτες του
άρα οι διαιρέτες του  είναι της μορφής
είναι της μορφής 
 και
και 

 αν
αν  άρτιος και
άρτιος και  αν
αν  περιττός.
περιττός. είναι
είναι 
 είναι
είναι 
 αρκεί
αρκεί  άρτιος.
άρτιος. άρτιο πρέπει
άρτιο πρέπει  άρτιος.
άρτιος.![\left [ 0,4022 \right ] \left [ 0,4022 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/e13d22cb51cfdea25e379e2e86781850.png) υπάρχουν
υπάρχουν  άρτιοι.
άρτιοι.![\left [ 0,2011 \right ] \left [ 0,2011 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/348badf98a5b8007b660eaef285edc79.png) υπάρχουν
υπάρχουν  άρτιοι.
άρτιοι. τέτοιοι διαιρέτες.
τέτοιοι διαιρέτες. περιττό πρέπει
περιττό πρέπει  περιττός
περιττός![\left [ 0,4022 \right ] \left [ 0,4022 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/e13d22cb51cfdea25e379e2e86781850.png) υπάρχουν
υπάρχουν  περιττοί.
περιττοί.![\left [ 0,2011 \right ] \left [ 0,2011 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/ca8bb86413a315ea70b3ec295a51e604.png) υπάρχουν
υπάρχουν  περιττοί.
περιττοί. διαιρέτες .
διαιρέτες .Νομίζω το ζητούμενο εδώ ήταν να λυθεί με την ακόλουθη πιο διαισθητική έννοια της πιθανότητας:Λάμπρος Κατσάπας έγραψε: ↑Σάβ Φεβ 23, 2019 9:37 pmαριθμός Γιώργου.
αριθμός Μαρίας.
συναρτήσεις πυκνότητας πιθανότητας των
και
, αντίστοιχα.
Η ζητούμενη πιθανότητα είναι

 πιθανότητα να ανήκει στο
πιθανότητα να ανήκει στο ![[0,2017] [0,2017]](/forum/ext/geomar/texintegr/latexrender/pictures/141eebf5c869568de5011ea127520e57.png) και
και  πιθανότητα να ανήκει στο
πιθανότητα να ανήκει στο ![[2017,4034] [2017,4034]](/forum/ext/geomar/texintegr/latexrender/pictures/dd4350f116334fd09f08177302f15a58.png) . Στην πρώτη περίπτωση από συμμετρία υπάρχει
. Στην πρώτη περίπτωση από συμμετρία υπάρχει  πιθανότητα ο αριθμός της Μαρίας να είναι μεγαλύτερος του Γιώργου. Στη δεύτερη περίπτωση ο αριθμός της Μαρίας είναι σίγουρα μεγαλύτερος από αυτόν του Γιώργου. Άρα η ζητούμενη πιθανότητα είναι:
πιθανότητα ο αριθμός της Μαρίας να είναι μεγαλύτερος του Γιώργου. Στη δεύτερη περίπτωση ο αριθμός της Μαρίας είναι σίγουρα μεγαλύτερος από αυτόν του Γιώργου. Άρα η ζητούμενη πιθανότητα είναι: 

 .
.  , παίρνοντας περιπτώσεις
, παίρνοντας περιπτώσεις  βλέπουμε πως ακριβώς ένας απο αυτούς θα έχει υπόλοιπο 1 και ο άλλος 2
βλέπουμε πως ακριβώς ένας απο αυτούς θα έχει υπόλοιπο 1 και ο άλλος 2  .
. ισούται με το πλήθος των διαιρετών με
ισούται με το πλήθος των διαιρετών με  , αλλιώς θα είχαμε δύο διαιρέτες με
, αλλιώς θα είχαμε δύο διαιρέτες με  .
.  και ισούται με
και ισούται με
Είναι
 . Αφού
. Αφού  ως αποτέλεσμα της
ως αποτέλεσμα της  , θα είναι
, θα είναι  . Δηλαδή,
. Δηλαδή,  .
. 
Έστω ένας παίκτηςsocrates έγραψε: ↑Σάβ Φεβ 23, 2019 12:44 pmΆσκηση 111
Ένας αριθμός ομάδων συμμετείχε σε ένα τουρνουά round-robin, δηλαδή ένα τουρνουά στο οποίο κάθε ομάδα έπαιξε με κάθε άλλη ακριβώς μια φορά. Κάθε ομάδα νίκησε σε ακριβώςπαιχνίδια και έχασε σε ακριβώς
παιχνίδια, ενώ δεν υπήρξαν ισοπαλίες. Πόσα σύνολα τριών ομάδων
υπάρχουν για τα οποία η
νίκησε την
, η
νίκησε την
και η
νίκησε την

 . Θα βρούμε σε πόσα τέτοια σύνολα ανήκει ο
. Θα βρούμε σε πόσα τέτοια σύνολα ανήκει ο  . Έστω
. Έστω  το σύνολο των
το σύνολο των  παικτών τους οποίους κέρδισε ο
παικτών τους οποίους κέρδισε ο  και
και  το σύνολο των
το σύνολο των  παικτών οι οποίοι κέρδισαν τον
παικτών οι οποίοι κέρδισαν τον  . Αναγκαστικά σε κάθε τριάδα της πιο πάνω μορφής πρέπει να έχουμε
. Αναγκαστικά σε κάθε τριάδα της πιο πάνω μορφής πρέπει να έχουμε  και
και  . Αρκεί λοιπόν να βρούμε πόσες κατευθυνόμενες ακμές υπάρχουν από το
. Αρκεί λοιπόν να βρούμε πόσες κατευθυνόμενες ακμές υπάρχουν από το  στο
στο  .
.  φεύγουν
φεύγουν  κατευθυνόμενες ακμές. Συνολικά έχουμε
κατευθυνόμενες ακμές. Συνολικά έχουμε  ακμές εκ των οποίων οι
ακμές εκ των οποίων οι  είναι μέσα στο
είναι μέσα στο  . Οι άλλες 55 αναγκαστικά πάνω από το
. Οι άλλες 55 αναγκαστικά πάνω από το  στο
στο  .
. τέτοιες τριάδες και έχουμε συνολικά
τέτοιες τριάδες και έχουμε συνολικά  τέτοιες τριάδες.
τέτοιες τριάδες. μαθητές , καθισμένοι σε
μαθητές , καθισμένοι σε  σειρές των
σειρές των  θρανίων . Κάποια στιγμή
θρανίων . Κάποια στιγμή μαθητές . Ποια είναι η πιθανότητα να βρίσκονται ανά
μαθητές . Ποια είναι η πιθανότητα να βρίσκονται ανά  σε κάθε σειρά ;
σε κάθε σειρά ;Είναι όσο το πλήθος των διαδρομών από τοKARKAR έγραψε: ↑Τετ Μάιος 29, 2019 7:37 pmΣε μια αίθουσα διαγωνίζονταιμαθητές , καθισμένοι σε
σειρές των
θρανίων . Κάποια στιγμή
έχουν μείνει στην αίθουσαμαθητές . Ποια είναι η πιθανότητα να βρίσκονται ανά
σε κάθε σειρά ;
Θεωρούμε ότι ο κάθε μαθητής έχει την ίδια πιθανότητα να είναι ο επόμενος που θα αναχωρήσει .
 έως το
έως το  προς το συνολικό πλήθος των διαδρομών που μπορούμε
προς το συνολικό πλήθος των διαδρομών που μπορούμε  στο
στο  είναι
είναι  .
. όπου η άθροιση εκτείνεται
όπου η άθροιση εκτείνεται 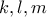 με
με  .
.  και επομένως η ζητούμενη πιθανότητα είναι
και επομένως η ζητούμενη πιθανότητα είναι 
 έτσι ώστε τόσο οι άρτιοι όσο και οι περιττοί να βρίσκονται σε αύξουσα σειρά;
έτσι ώστε τόσο οι άρτιοι όσο και οι περιττοί να βρίσκονται σε αύξουσα σειρά;Έστωsocrates έγραψε: ↑Τετ Μαρ 25, 2020 4:56 pmΆσκηση 112
Βάφουμε τους αριθμούς 1, 2, 3, ...,20 με δύο χρώματα άσπρο και μαύρο έτσι, ώστε να
χρησιμοποιούνται και τα δύο χρώματα. Με πόσους τρόπους μπορεί να γίνει ο
χρωματισμός ώστε το γινόμενο των άσπρων αριθμών και το γινόμενο των μαύρων
αριθμών να έχουν μέγιστο κοινό διαιρέτη ίσο με 1;
 το σύνολο με στοιχεία τους άσπρους και μαύρους αντίστοιχα αριθμούς.
το σύνολο με στοιχεία τους άσπρους και μαύρους αντίστοιχα αριθμούς. θα πρέπει να βρίσκονται στο ίδιο σύνολο.
θα πρέπει να βρίσκονται στο ίδιο σύνολο. πάνε μαζί.Όμως μαζί τους παίρνουν και τους
πάνε μαζί.Όμως μαζί τους παίρνουν και τους  .
. στα
στα  ώστε
ώστε  .
.
 τρόποι.
τρόποι. τρόποι.
τρόποι. τρόποι
τρόποι τρόποι.
τρόποι.Έστωsocrates έγραψε: ↑Τετ Δεκ 02, 2020 2:35 amΆσκηση 114
Ο Κώστας έχει ένα χρηματοκιβώτιο το οποίο ξεκλειδώνει με έναν τριψήφιο αριθμό. Ξέχασε όμως τον αριθμό αυτό. Το μόνο που θυμάται είναι ότι αποτελείται μόνο από περιττά, διαφορετικά μεταξύ τους, ψηφία και ότι διαιρείται με το 3. O μέγιστος αριθμός δοκιμών που μπορεί να κάνει ώστε να ξεκλειδώσει το χρηματοκιβώτιο είναι:
 ο τριψήφιος με
ο τριψήφιος με  περιττούς και
περιττούς και 
 είναι περιττός.
είναι περιττός.
 αδύνατο διότι
αδύνατο διότι  διαφορετικοί ανά
διαφορετικοί ανά 
 και όλες οι μεταθέσεις τους*
και όλες οι μεταθέσεις τους* ή
ή  και όλες οι μεταθέσεις τους*
και όλες οι μεταθέσεις τους* και όλες οι μεταθέσεις τους*
και όλες οι μεταθέσεις τους* αδύνατο
αδύνατο το πολύ δοκιμές
το πολύ δοκιμέςΓενικότερα για
 αριθμούς είναι:
αριθμούς είναι: άρτιους και τους τοποθετούμε σε
άρτιους και τους τοποθετούμε σε  από τις
από τις  θέσεις με αύξουσα σειρά με
θέσεις με αύξουσα σειρά με  τρόπους.
τρόπους. θέσεις τοποθετούμε σε αύξουσα σειρά τους περιττούς
θέσεις τοποθετούμε σε αύξουσα σειρά τους περιττούς τρόποι
τρόποι τρόπους.
τρόπους.Έστω ότιsocrates έγραψε: ↑Τετ Δεκ 02, 2020 2:35 amΆσκηση 115
Ρωτήσαμε τα άτομα που παρευρίσκονται σε ένα καφενείο ποιες εφημερίδες διαβάζουν από τις A, B και Γ. Σύμφωνα με τις απαντήσεις τους, κανένας δεν διαβάζει ακριβώς δύο από αυτές, 7 διαβάζουν την Α εφημερίδα, 8 τη Β εφημερίδα, αλλά αυτοί που διαβάζουν μόνο τη Γ εφημερίδα είναι διπλάσιοι από αυτούς που διαβάζουν και τις τρεις. Να βρείτε πόσοι από αυτούς διαβάζουν μόνο μια εφημερίδα.
 άτομα διαβάζουν και τις
άτομα διαβάζουν και τις  εφημερίδες
εφημερίδες  άτομα διαβάζουν μόνο τη Γ εφημερίδα
άτομα διαβάζουν μόνο τη Γ εφημερίδα διαβάζουν μόνο την Α,
διαβάζουν μόνο την Α,  διαβάζουν μόνο τη Β και
διαβάζουν μόνο τη Β και  διαβάζουν μόνο τη Γ
διαβάζουν μόνο τη Γ άτομα διαβάζουν από μία εφημερίδα
άτομα διαβάζουν από μία εφημερίδα άτομα διαβάζουν την
άτομα διαβάζουν την  και
και  την
την  , τότε
, τότε  άτομα διαβάζουν από μία εφημερίδα
άτομα διαβάζουν από μία εφημερίδα (οι φυσικοί αριθμοί από το
(οι φυσικοί αριθμοί από το  μέχρι το
μέχρι το  ), με πόσους τρόπους μπορούν να επιλεγούν τρεις διαφορετικοί αριθμοί από το σύνολο
), με πόσους τρόπους μπορούν να επιλεγούν τρεις διαφορετικοί αριθμοί από το σύνολο  ώστε το άθροισμά τους να είναι δαιρετό με το
ώστε το άθροισμά τους να είναι δαιρετό με το  ;
;Δεν είναι σαφές από την εκφώνηση αν οι αναδιατάξεις μιάς τριάδας αριθμών μετράει ως η ίδια επιλογή ή διαφορετική. Π.χ. είναι η
 πολ/σιο του
πολ/σιο του  ίδια με την
ίδια με την  ; Επιλέγουμε τι μας αρέσει. Ας πούμε ότι αποφασίζουμε να μετρήσουμε τις διατεταγμένες τριάδες (όμοια η άλλη επιλογή).
; Επιλέγουμε τι μας αρέσει. Ας πούμε ότι αποφασίζουμε να μετρήσουμε τις διατεταγμένες τριάδες (όμοια η άλλη επιλογή).  είναι, κατά σειρά,
είναι, κατά σειρά,  (είναι δέκα από το κάθε είδος). Το άθροισμα τριών αριθμών είναι πολλαπλάσιο του
(είναι δέκα από το κάθε είδος). Το άθροισμα τριών αριθμών είναι πολλαπλάσιο του  αν και μόνον αν η τριάδα τους είναι της μορφής
αν και μόνον αν η τριάδα τους είναι της μορφής  ή της
ή της  ή της
ή της  ή της
ή της  (με κάποια σειρά).
(με κάποια σειρά).  επιλογές. Όμοια οι υπόλοιπες. Το αφήνω ως ρουτίνα.
επιλογές. Όμοια οι υπόλοιπες. Το αφήνω ως ρουτίνα. μαθητές θέλουμε να δώσουμε
μαθητές θέλουμε να δώσουμε  βιβλία, ώστε κάθε παιδί να πάρει τουλάχιστον
βιβλία, ώστε κάθε παιδί να πάρει τουλάχιστον  βιβλίο.
βιβλίο. τρόπους
τρόπους τρόπους
τρόπους τρόποι
τρόποιΓιώργο, καλησπέρα !
 που έχεις μπροστά και τι το κλάσμα ;
που έχεις μπροστά και τι το κλάσμα ;Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες