Πολύ ωραία η λύση σου, Δημήτρη. Ευχαριστούμε.dement έγραψε: 2. Για καθεισχυει οτι
και
.
Ας μου επιτρέψεις να εξηγήσω λίγο αναλυτικότερα (εννοώ αυτό το "λίγο" γιατί βιάζομαι!) το βήμα που σημείωσα, γιατί δεν είναι ... τεριμμένο:
Κάθε πίνακας ικανοποιεί την χαρακτηριστική του εξίσωση, από Cayley-Hamilton. Για 2χ2 πίνακες είναι Α^2 - [tr(A)]A + (detA)I = 0 (*).
Εδώ det(A) = 1, και tr(A) = το ίχνος = το άθροισμα των στοιχίων της διαγωνίου.
Παίρνοντας το ίχνος (είναι γραμμική απεικόνιση από το σύνολο των 2χ2 πινάκων στους πραγματικούς) έχουμε την πρώτη εξίσωση. Υψώνοντας στο τεράγωνο και αντικαθιστώντας το Α^2 από την (*), έχουμε την δεύτερη.
Φιλικά,
Μιχάλης Λάμπρου

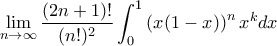 , όπου
, όπου  .
. , όπου
, όπου ![f:[0,1] \to \mathbb{R} f:[0,1] \to \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/d961f003d1b32deb05785be107ca82fb.png) είναι μία συνεχής συνάρτηση.
είναι μία συνεχής συνάρτηση.
 (οπου
(οπου  ο διωνυμικος συντελεστης). Το οριο του πρωτου παραγοντα ειναι
ο διωνυμικος συντελεστης). Το οριο του πρωτου παραγοντα ειναι  και δεν τον ξαναγραφουμε. Το αντιστροφο του δευτερου παραγοντα ισουται με
και δεν τον ξαναγραφουμε. Το αντιστροφο του δευτερου παραγοντα ισουται με  . Καθενα απο τα (πεπερασμενου πληθους) πηλικα ειναι ρητη συναρτηση που τεινει στο
. Καθενα απο τα (πεπερασμενου πληθους) πηλικα ειναι ρητη συναρτηση που τεινει στο  και το αρχικο οριο ειναι
και το αρχικο οριο ειναι  (αφου ειχαμε παρει το αντιστροφο).
(αφου ειχαμε παρει το αντιστροφο).  ειναι συνεχης σε συμπαγες συνολο, οποτε φραγμενη. Εστω
ειναι συνεχης σε συμπαγες συνολο, οποτε φραγμενη. Εστω  ενα φραγμα της.
ενα φραγμα της.  . Παρατηρουμε τα εξης :
. Παρατηρουμε τα εξης : ειναι γνησιως αυξουσα στο
ειναι γνησιως αυξουσα στο ![[0,1/2] [0,1/2]](/forum/ext/geomar/texintegr/latexrender/pictures/f8c2fdd9788155314d87d62c261ac20f.png) και γνησιως φθινουσα στο
και γνησιως φθινουσα στο ![[1/2,1] [1/2,1]](/forum/ext/geomar/texintegr/latexrender/pictures/79a4728c28ca356c3993dc909dedc09f.png) για καθε
για καθε  .
. για καθε
για καθε  για καθε
για καθε ![x \in [0,1] - \{1/2\} x \in [0,1] - \{1/2\}](/forum/ext/geomar/texintegr/latexrender/pictures/6fe118215004b3caa3df89c0eb958466.png) (απο το γεγονος οτι
(απο το γεγονος οτι  ).
). .
. , με σταθερο ολοκληρωμα. Διαισθητικα βλεπουμε οτι το οριο πρεπει να ειναι το
, με σταθερο ολοκληρωμα. Διαισθητικα βλεπουμε οτι το οριο πρεπει να ειναι το  .
.  . Παιρνουμε το αναλογο
. Παιρνουμε το αναλογο  (απο τη συνεχεια) γυρω απο το
(απο τη συνεχεια) γυρω απο το  και επιλεγουμε
και επιλεγουμε  τετοιο ωστε
τετοιο ωστε 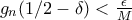 για καθε
για καθε  . Θετουμε
. Θετουμε  . Ισχυει
. Ισχυει  στο
στο ![[1/2 - \delta, 1/2 + \delta] [1/2 - \delta, 1/2 + \delta]](/forum/ext/geomar/texintegr/latexrender/pictures/e2bfe420515c13759594fe477431d395.png) (εκ κατασκευης) και
(εκ κατασκευης) και  (απο το φραγμα) οπουδηποτε αλλου. Εχουμε οτι :
(απο το φραγμα) οπουδηποτε αλλου. Εχουμε οτι :
 . Αρα το οριο ειναι πραγματι το
. Αρα το οριο ειναι πραγματι το ![f:[0,1]\times [0,1]\to {\mathbb R} f:[0,1]\times [0,1]\to {\mathbb R}](/forum/ext/geomar/texintegr/latexrender/pictures/69f50967e9384b9ecd3be9e54bbff23b.png) . Να βρεθεί το
. Να βρεθεί το  .
. αλλά μάλλον πρόκειται για τυπογραφικό.
αλλά μάλλον πρόκειται για τυπογραφικό.