 καλό αν υπάρχει μια άπειρη ακολουθία
καλό αν υπάρχει μια άπειρη ακολουθία 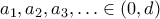 έτσι ώστε για κάθε
έτσι ώστε για κάθε  τα σημεία
τα σημεία 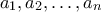 διαμερίζουν το διάστημα
διαμερίζουν το διάστημα ![[0,d] [0,d]](/forum/ext/geomar/texintegr/latexrender/pictures/c16685098b1b281653b2cfe08bfaaa5b.png) σε τμήματα μήκους το πολύ
σε τμήματα μήκους το πολύ 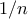 το κάθε ένα.
το κάθε ένα.Να βρεθεί το
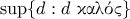
Συντονιστής: Demetres
 καλό αν υπάρχει μια άπειρη ακολουθία
καλό αν υπάρχει μια άπειρη ακολουθία 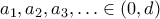 έτσι ώστε για κάθε
έτσι ώστε για κάθε  τα σημεία
τα σημεία 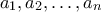 διαμερίζουν το διάστημα
διαμερίζουν το διάστημα ![[0,d] [0,d]](/forum/ext/geomar/texintegr/latexrender/pictures/c16685098b1b281653b2cfe08bfaaa5b.png) σε τμήματα μήκους το πολύ
σε τμήματα μήκους το πολύ 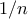 το κάθε ένα.
το κάθε ένα.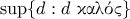
Η απάντηση είναι
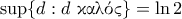 .
. είναι καλός τότε
είναι καλός τότε  .
. , έστω
, έστω  η αναδιάταξη των
η αναδιάταξη των  τέτοια ώστε
τέτοια ώστε 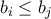 αν
αν 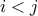 . Έστω επίσης
. Έστω επίσης 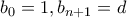 και
και 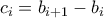 για
για 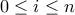 . Τότε είναι
. Τότε είναι 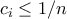 για κάθε
για κάθε  .
. πρέπει τα
πρέπει τα  διαστήματα που δημιουργούνται να είναι όλα μήκους το πολύ
διαστήματα που δημιουργούνται να είναι όλα μήκους το πολύ 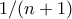 . Όμως, με την προσθήκη μόνο ενός στοιχείου, ακριβώς
. Όμως, με την προσθήκη μόνο ενός στοιχείου, ακριβώς  από τα
από τα  διαστήματα που είχαμε πριν θα παραμείνουν του ίδιου μήκους. Οπότε για τουλάχιστον
διαστήματα που είχαμε πριν θα παραμείνουν του ίδιου μήκους. Οπότε για τουλάχιστον  δείκτες
δείκτες  ισχύει
ισχύει 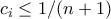 .
.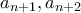 τουλάχιστον
τουλάχιστον  από τα
από τα  διαστήματα που είχαμε πριν θα παραμείνουν του ίδιου μήκους, οπότε για τουλάχιστον
διαστήματα που είχαμε πριν θα παραμείνουν του ίδιου μήκους, οπότε για τουλάχιστον  δείκτες
δείκτες  ισχύει
ισχύει  .
. δείκτες
δείκτες  ισχύει
ισχύει 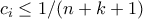 , με
, με 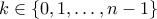 .
.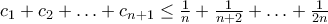 . Όμως είναι
. Όμως είναι 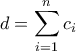 , άρα
, άρα 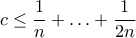 .
.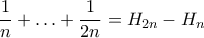 , και
, και 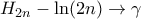 ,
, 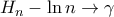 , (όπου
, (όπου  η σταθερά Euler-Mascheroni), άρα και
η σταθερά Euler-Mascheroni), άρα και 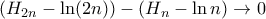 , οπότε
, οπότε 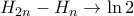 για
για 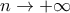 , συνεπώς
, συνεπώς  , όπως θέλαμε.
, όπως θέλαμε.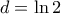 είναι καλός. Αποδεικνύουμε το εξής:
είναι καλός. Αποδεικνύουμε το εξής: ώστε, μετά την επιλογή των
ώστε, μετά την επιλογή των 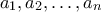 , τα
, τα  διαστήματα που δημιουργούνται να είναι μήκους
διαστήματα που δημιουργούνται να είναι μήκους 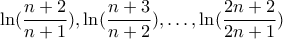 , για κάθε
, για κάθε  .
.  είναι προφανές. Έστω ότι για
είναι προφανές. Έστω ότι για 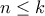 έχουμε επιλέξει κατάλληλα τα
έχουμε επιλέξει κατάλληλα τα 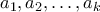 . Τότε, έχουμε
. Τότε, έχουμε  τμήματα μήκους:
τμήματα μήκους: , και θέλουμε να προσθέσουμε το
, και θέλουμε να προσθέσουμε το  έτσι ώστε να προκύψουν
έτσι ώστε να προκύψουν  τμήματα μήκους
τμήματα μήκους . Αυτό μπορούμε να το πετύχουμε αν ''σπάσουμε'' το τμήμα μήκους
. Αυτό μπορούμε να το πετύχουμε αν ''σπάσουμε'' το τμήμα μήκους  σε δύο τμήματα μήκους
σε δύο τμήματα μήκους 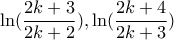 .
. 
 , για κάθε
, για κάθε  . Προφανώς το αριστερό μέλος ισούται με
. Προφανώς το αριστερό μέλος ισούται με 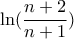 (όλα τα στοιχεία είναι της μορφής
(όλα τα στοιχεία είναι της μορφής 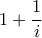 με
με 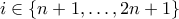 και αυτό γίνεται μέγιστο για
και αυτό γίνεται μέγιστο για  ), και είναι:
), και είναι: , και τελειώσαμε.
, και τελειώσαμε.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 23 επισκέπτες