 πίνακας
πίνακας  ώστε
ώστε 
(α) Να δειχθεί ότι υπάρχει μοναδικός πραγματικός
 πίνακας
πίνακας  που ικανοποιεί την εξίσωση
που ικανοποιεί την εξίσωση 
(β) Να εκφραστεί ο
 σε σχέση με τον
σε σχέση με τον  .
.Συντονιστής: Demetres
 πίνακας
πίνακας  ώστε
ώστε 
 πίνακας
πίνακας  που ικανοποιεί την εξίσωση
που ικανοποιεί την εξίσωση 
 σε σχέση με τον
σε σχέση με τον  .
. . Μετά απλώς επαληθεύουμε το α) και η μοναδικότητα είναι απλή.
. Μετά απλώς επαληθεύουμε το α) και η μοναδικότητα είναι απλή. βρίσκουμε
βρίσκουμε 
 παίρνουμε
παίρνουμε  . Αντικαθιστώντας στην προηγούμενη παίρνουμε
. Αντικαθιστώντας στην προηγούμενη παίρνουμε 
 από αριστερά παίρνουμε
από αριστερά παίρνουμε  , οπότε
, οπότε  .
.  . Αρκεί τώρα να είναι αντιστρέψιμος ο
. Αρκεί τώρα να είναι αντιστρέψιμος ο  . Με την πληροφορία που έχουμε για τον
. Με την πληροφορία που έχουμε για τον  , σκεπτόμαστε την ταυτότητα
, σκεπτόμαστε την ταυτότητα 
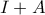 είναι αντιστρέψιμος και ο αντίστροφός του είναι ο
είναι αντιστρέψιμος και ο αντίστροφός του είναι ο  . Επομένως
. Επομένως 
Νομίζω ότι είναι πολύ γνωστό πρόβλημα.




 που κάνει το αρχικό πρόβλημα πολύ πιο εύκολο
που κάνει το αρχικό πρόβλημα πολύ πιο εύκολοΚαλημέρα!ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Πέμ Αύγ 12, 2021 11:45 pmΝομίζω ότι είναι πολύ γνωστό πρόβλημα.
(παρόμοιο εμφανίζεται στις εξετάσεις Γραμμικής 1 στο Μαθηματικό Αθηνών)
Είναι
Η
γράφεται
Ετσι
και τελειώσαμε και για τα δύο.
 Νομίζω χρειάζεται απόδειξη.
Νομίζω χρειάζεται απόδειξη. Καλημέρα.achilleas έγραψε: ↑Παρ Αύγ 13, 2021 10:45 amΚαλημέρα!ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Πέμ Αύγ 12, 2021 11:45 pmΝομίζω ότι είναι πολύ γνωστό πρόβλημα.
(παρόμοιο εμφανίζεται στις εξετάσεις Γραμμικής 1 στο Μαθηματικό Αθηνών)
Είναι
Η
γράφεται
Ετσι
και τελειώσαμε και για τα δύο.
Γιατί ισχύειΝομίζω χρειάζεται απόδειξη.
Φιλικά,
Αχιλλέας
 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες