 η ακολουθία Fibonacci η οποία ορίζεται ως
η ακολουθία Fibonacci η οποία ορίζεται ως  ,
,  και για
και για  ισχύει
ισχύει  . Να δειχθεί ότι:
. Να δειχθεί ότι:
Συντονιστής: Demetres
 ως
ως  αφού για
αφού για 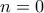 ο παράγοντας είναι ίσος με
ο παράγοντας είναι ίσος με  .
.  με
με  και
και 



 , έχουμε
, έχουμε
 και
και 

 το ζητούμενο έπεται.
το ζητούμενο έπεται.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες