3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Summand · #1

Καλησπέρα! Παραθέτω τα θέματα του παραπάνω διαγωνισμού που διεξήχθη σήμερα στο Τουρκμενιστάν. Επιπλέον μπορούσαν να συμμετέχουν φοιτητές από όλο τον κόσμο μέσω διαδικτύου. Υπήρχαν δύο κατηγορίες. Στην πρώτη διαγωνίζονταν φοιτητές Μαθηματικών και Επιστήμης Υπολογιστών και στην δεύτερη οι υπόλοιποι. Τα προβλήματα ήταν στα αγγλικά και ήταν σχετικά κακομεταφρασμένα, παρ' όλ' αυτά αξίζει να τους ρίξουμε μια ματιά! Περισσότερες πληροφορίες υπάρχουν εδώ.

Α΄ Κατηγορία

Πρόβλημα 1: Μυρμήγκια κάθονται σε κάθε μια από τις κορυφές $A_i \ (i=1,2,...,n)$ και στο κέντρο

ενός κανονικού ν-γώνου. Τα μυρμήγκια ξεκινούν να κινούνται κατά μήκος των πλευρών του ν-γώνου και κατά μήκος των γραμμών $A_iO \ (i=1,2,...,n)$ . Υπολογίστε την πιθανότητα να μη συναντηθούν τα μυρμήγκια.

Πρόβλημα 2: Έστω ${x_{n}}$ ακολουθία τέτοια ώστε x_0=1

και $x_n=\frac{x_{n-1}}{x_{n-1}^{2}+x_{n-1}+1}, n\geq 1$ . Αποδείξτε ότι η ακολουθία ${nx_{n}}$ συγκλίνει και βρείτε το όριο της.

Πρόβλημα 3: Έστω $A,B\in M_{n}(\mathbb{R})$ πίνακες τέτοιοι ώστε AB-A-B=I

και $A=-A^{T}$ . Αποδείξτε ότι:
a) Οι πίνακες I-A,I-B

είναι αντιστρέψιμοι.
b) Ο πίνακας

είναι ορθογώνιος.

Πρόβλημα 4: Έστω $n\in\mathbb{N}$ . Για κάθε πρώτο p>3

αποδείξτε ότι $C_{np}^{p}-C_{np}^{2p}+\cdots+(-1)^{n-1}C_{np}^{np}\equiv 1\ (mod\ p^{3})$ όπου $C_{n}^{k}=\frac{n!}{(n-k)!k!}$

Πρόβλημα 5: Έστω

μια πεπερασμένη ομάδα και

δεύτερης τάξης αυτομορφισμός της. Αν το μοναδικό σταθερό σημείο του

είναι το μοναδιαίο στοιχείο της

, τότε να δείξετε ότι η

είναι αβελιανή ομάδα.

Πρόβλημα 6: Είναι δυνατό στον Ευκλείδειο χώρο 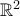$\mathbb{R}^{2}$ ένα αριθμήσιμο σύνολο μεμονωμένων σημείων να έχει μη υπεραριθμήσιμα συσσώρευσης;

Β΄ Κατηγορία

Πρόβλημα 1: Τρεις ψαράδες θέλουν να μοιράσουν την ψαριά τους όμως δεν έχουν ζυγαριές. Ο καθένας είναι σίγουρος ότι χωρίζει την ψαριά σε τρία ίσα μέρη, άλλα οι υπόλοιποι δεν τον εμπιστεύονται. Αν υπήρχαν μόνο δύο ψαράδες, η λύση για να βγούμε από αυτή την κατάσταση θα ήταν απλή: ο ένας θα χώριζε την ψαριά σε δύο μέρη και ο άλλος θα διάλεγε εκείνο το μέρος που θα του φαινόταν μεγαλύτερο. Υποδείξτε τον τρόπο με τον οποίο πρέπει να γίνει η μοιρασιά, ώστε καθένας να είναι σίγουρος ότι πήρε τουλάχιστον το $\frac{1}{3}$ της συνολικής ψαριάς. (Εδώ δόθηκε διευκρίνηση, ότι, ουσιαστικά, ζητείται ο τρόπος με τον οποίο όλοι θα είναι ευχαριστημένοι. Θεωρούμε δηλαδή ότι στην περίπτωση των δύο ατόμων που περιγράφεται στο τέλος παίρνουν από μισά.)

Πρόβλημα 2: Έστω ${a_{n}}$ ακολουθία τέτοια ώστε $a_{0}=1, a_{1}=2, a_{n+1}=\frac{3^{n-1}+a_{n}^{2}}{a_{n-1}},n\geq 1$
a) Δείξτε ότι οι αριθμοί $a_{n}$ είναι ακέραιοι.
b) Συγκλίνει η σειρά $\sum_{n=0}^{\infty }\frac{1}{a_{n}}$ ;
c) Συγκλίνει η σειρά $\sum_{n=0}^{\infty }\frac{a_{n+1}}{a_{n}}$ ;

Πρόβλημα 3: Θεωρούμε στο επίπεδο τα σημεία O, A, A_1, A_2

τα οποία βρίσκονται πάνω στην ευθεία l_1

, τα σημεία O,B,B_1,B_2

τα οποία βρίσκονται πάνω στην ευθεία l_2

και τέτοια ώστε OA>OB, AA_1=BB_1, A_1A_2=B_1B_2

a) (Το παραθέτω αυτούσιο στα αγγλικά, αφού αδυνατώ να κατανοήσω τι ζητείται) Prove that on circles triangles OAB, OA1B1 and OA2B2 has common point M.
b) Αν C,C_1,C_2

είναι τα μέσα των τμημάτων AB,A_1B_1,A_2B_2

, αποδείξτε ότι τα C,C_1,C_2

είναι συνευθειακά και βρίσκονται πάνω σε ευθεία

.
c) Αν $l\cap l_1=P$ , αποδείξτε ότι $l_1\perp MP$ .

Πρόβλημα 4: Έστω $A=(a_{ij})$ ένας αντισυμμετρικός πίνακας με στοιχεία πραγματικούς αριθμούς τέτοιος ώστε det(A)=2020

. Έστω $B=(b_{ij})$ πίνακας με στοιχεία πραγματικούς αριθμούς τέτοια ώστε $b_{ij}=a_{ij}+2021$ . Να βρεθούν όλες οι δυνατές τιμές του det(B)

.

Πρόβλημα 5: Να υπολογιστεί το ολοκλήρωμα $\int_{0}^{\frac{\pi}{4}}arctan(\sqrt{\frac{1}{2}(1-tan^{2}x)})dx$

Πρόβλημα 6: Να αποδειχτεί ότι για κάθε θετικό ακέραιο $n\geq 3$ υπάρχουν

διακριτά σημεία στο επίπεδο, όχι συνευθειακά, ώστε όλες οι ανά δύο αποστάσεις μεταξύ των σημείων αυτών είναι ακέραιοι αριθμοί.

Φιλικά,
Γιάννης

Λάμπρος Κατσάπας · #2

Υπάρχουν προβλήματα στη μετάφραση. Π.χ. ένα που πέτυχα είναι το πρόβλημα 6 στην κατηγορία Α. Το μετρήσιμο σύνολο να γίνει αριθμήσιμο σύνολο και το μη μετρήσιμα να γίνει υπεραριθμήσιμο πλήθος.

sot arm · #3

Summand έγραψε: ↑
Κυρ Μαρ 22, 2020 7:00 pm

Πρόβλημα 5: Έστω μια πεπερασμένη ομάδα και δεύτερης τάξης αυτομορφισμός της. Αν το μοναδικό σταθερό σημείο του είναι το μοναδιαίο στοιχείο της , τότε να δείξετε ότι η είναι αβελιανή ομάδα.

Μου φάνηκε ωραίο πρόβλημα:

Ισχυρισμός: $\forall g \in G , \exists x \in G, g=x^{-1}f(x)$

Για να το δείξουμε αυτό, αρκεί να δείξουμε ότι η απεικόνιση: $x \rightarrow x^{-1}f(x)$ είναι επί της

.

Επειδή η

είναι αυτομορφισμός και η ομάδα

πεπερασμένη, αρκεί να δείξω πως είναι '1-1'

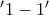. Έστω λοιπόν $x,y \in G$ με:

$\displaystyle{x^{-1}f(x)=y^{-1}f(y)\Rightarrow f(x^{-1})f(f(x))=f(y^{-1})f(f(y)) \Rightarrow f(y)f(x^{-1})=yx^{-1} \Rightarrow f(yx^{-1})=yx^{-1} \Rightarrow yx^{-1}=e \Rightarrow y=x}$

Αφού το

είναι το μόνο σταθερό σημείο της f.

Άρα αν $g \in G$ :

$\displaystyle{f(g)=f(x^{-1}f(x))=...=[x^{-1}f(x)]^{-1}=g^{-1}}$

Τέλος, αν $a,b \in G$ , από το γεγονός πως :

f(ab)=f(a)f(b)

και ότι $f(g)=g^{-1}$ και με απλές πράξεις προκύπτει ότι η

είναι Αβελιανή.

Σχόλιο: Νομίζω πως ήταν πολλά για ένα τετράωρο μαζί με στο σκανάρισμα, το γράψιμο και το να σταλθούν έχοντας ένα εύλογο χρονικό περιθώριο.

#4

Summand έγραψε: ↑
Κυρ Μαρ 22, 2020 7:00 pm

Πρόβλημα 3: Έστω $A,B\in M_{n}(\mathbb{R})$ πίνακες τέτοιοι ώστε και $A=-A^{T}$ . Αποδείξτε ότι:
a) Οι πίνακες είναι αντιστρέψιμοι.
b) Ο πίνακας είναι ορθογώνιος.

Τέτοιες ασκήσεις πέφτανε παλαιότερα στις Πανελλαδικές.

α) Ο αντίστροφος του I-A

είναι ο $\frac {1}{2} (I-B)$ καθώς από τον δοθείσα

$\displaystyle{\frac {1}{2} (I-A)(I-B) = \frac {1}{2} (I-A-B+AB)= \frac {1}{2} (I+I)=I}$ . Άρα o $\frac {1}{2} (I-B)$ είναι δεξί αντίστροφος, οπότε (από θεωρία) και αριστερός.

β) Η δοθείσα γράφεται -(I-A)B = I+A

. Άρα $B= -(I-A)^{-1}(I+A)$ , οπότε

$B^T= -(I+A)^T[(I-A)^{-1}]^T=-(I+A)^T{(I-A)^T]^{-1} = -(I+A^T)[(I-A^T)]^{-1}= -(I-A)(I+A)^{-1}$

Έπεται $\displaystyle{BB^T= +(I-A)^{-1}(I+A)(I-A)(I+A)^{-1} =(I-A)^{-1}(I-A)(I+A)(I+A)^{-1}= I\cdot I = I}$ , και λοιπά.

Summand · #5

Λάμπρος Κατσάπας έγραψε: ↑
Κυρ Μαρ 22, 2020 7:30 pm
Υπάρχουν προβλήματα στη μετάφραση. Π.χ. ένα που πέτυχα είναι το πρόβλημα 6 στην κατηγορία Α. Το μετρήσιμο σύνολο να γίνει αριθμήσιμο σύνολο και το μη μετρήσιμα να γίνει υπεραριθμήσιμο πλήθος.

Έχετε δίκιο, αφηρημάδα μάλλον, το διορθώνω αμέσως.

ChrP · #6

Πρόβλημα 2: Έστω ${x_{n}}$ ακολουθία τέτοια ώστε και $x_n=\frac{x_{n-1}}{x_{n-1}^{2}+x_{n-1}+1}, n\geq 1$ . Αποδείξτε ότι η ακολουθία ${nx_{n}}$ συγκλίνει και βρείτε το όριο της

Έστω $f(x_{n-1})=x_{n}$ με $f(x)=\frac{x}{x^2+x+1}$ τότε $f'(x)= \frac{x^2+x+1-x(2x+1)}{(x^2+x+1)^2}$ αρα $|f΄(x)|=|\frac{1-x^2}{(x^2+x+1)^2} |\leq 1$ (Η τελευταία ανισότητα προκύπτει από $|1-x^2| \leq |(x^2+x+1)^2 |$ , .Άρα η f είναι συστολή Lipchitz και είναι γνωστό ότι η f έχει μοναδικό σταθερό σημείο $f(l)=\lim_{n\to \infty}f(x_n)= \lim_{n\to \infty}x_n=l$ (Banach fixed point theorem )
Αρα τελικά x_n

συγγλινει .βάζοντας όρια στην σχέση έχουμε $l=\frac{l}{l^2+l+1}$ που δίνει l=0

η

το οποίο απορρίπτεται αφού x_n

θετική με επαγωγή
Τώρα αντί για την nx_n

θα μελετήσουμε την $\frac{1}{nx_n}$
$\frac{1}{nx_n}=\frac{\frac{1}{x_n}}{n}$
Από λήμμα stolz-cesaro το ζητούμενο όριο θα είναι ίσο με το $\frac{1}{x_{n+1}}-\frac{1}{x_n}= =\frac{x_{n}^{2}+x_{n}+1}{x_n}- \frac{1}{x_n}=x_n+1 \rightarrow 1$
Άρα τελικά $nx_n \rightarrow 1$

*Μετά την παρατήρηση του κυρίου Σταύρου δεν δουλεύει το Banach fix point άρα

$\frac{x_n}{x_{n-1}}=\frac{1}{x_{n-1}^2+x_{n-1}+1}$
Όμως $x_{n-1}^2+x_{n-1}+1 \geq 1$ αφού η x_n

θετική με επαγωγή άρα $\frac{x_n}{x_{n-1}}= \frac{1}{x_{n-1}^2+x_{n-1}+1}\leq 1$ άρα x_n

φθίνουσα και κάτω φραγμένη από το 0 άρα συγγλινει τα υπόλοιπα μένουν ίδια

#7

Summand έγραψε: ↑
Κυρ Μαρ 22, 2020 7:00 pm
Πρόβλημα 6: Να αποδειχτεί ότι για κάθε θετικό ακέραιο $n\geq 3$ υπάρχουν διακριτά σημεία στο επίπεδο, όχι συνευθειακά, ώστε όλες οι ανά δύο αποστάσεις μεταξύ των σημείων αυτών είναι ακέραιοι αριθμοί.

Για όσους ακεραίους $k,\,m,\, n,...$ θέλουμε, εξετάζουμε τα (συνευθειακά) σημεία $\displaystyle{\left ( \dfrac { 2k}{k^2-1}, \, 0\right ), \, \left ( \dfrac { 2m}{m^2-1}, \, 0\right ), \left ( \dfrac { 2n}{n^2-1}, \, 0\right ),...}$ . Οι μεταξύ τους αποστάσεις είναι βέβαια κάποιοι ρητοί αριθμοί.

Στον κατάλογό μας προσθέτουμε το σημείο (0,1)

. Τώρα τα σημεία μας δεν είναι συνευθειακά. Η απόσταση του νέου σημείου από το τυπικό από τα υπόλοιπα είναι

$\displaystyle{\sqrt { \left ( \dfrac { 2k}{k^2-1}\right )^2+1^2 }= \dfrac { k^2+1}{k^2-1}=}$ ρητός.

Με άλλα λόγια βρήκαμε όσα σημεία θέλουμε, με ρητές αποστάσεις μεταξύ τους. Πολλαπλασιάζουμε τώρα τα πάντα με έναν μεγάλο ακέραιο (το γινόμενο των παρονομαστών μας αρκεί) και πετυχαίνουμε ακέραιες αποστάσεις μεταξύ τους, όπως θέλαμε.

Tolaso J Kos · #8

Summand έγραψε: ↑
Κυρ Μαρ 22, 2020 7:00 pm

Πρόβλημα 5: Να υπολογιστεί το ολοκλήρωμα $\int_{0}^{\frac{\pi}{4}}arctan(\sqrt{\frac{1}{2}(1-tan^{2}x)})dx$

Δύσκολο!

$\displaystyle{\begin{aligned} \int_{0}^{\pi/4} \arctan \sqrt{\frac{1-\tan^2 t}{2}}\, \mathrm{d}t &\overset{1-\tan^2 t \mapsto 2t^2}{=\! =\! =\! =\! =\! =\!=\!=\!} \int_{0}^{\sqrt{2}/2} \frac{t \arctan t}{\sqrt{1-2t^2} \left ( 1-t^2 \right )} \, \mathrm{d}t \\ &=\cancelto{0}{\left [ - \arctan \sqrt{1-2t^2} \arctan t \right ]_0^{\sqrt{2}/2}} + \int_{0}^{\sqrt{2}/2} \frac{\arctan \sqrt{1-2t^2}}{1+t^2} \, \mathrm{d}t \end{aligned}}$
Φτάνω μέχρι εδώ, αλλά κωλύομαι! Καμία υπόδειξη;

Έχω στο νου μου το DUTIS ότι μάλλον θα χρειαστεί, αλλά πού θα εισάγω τη παράμετρο για τη παραγώγιση;

Tolaso J Kos · #9

Tolaso J Kos έγραψε: ↑
Δευ Μαρ 23, 2020 1:08 am

Summand έγραψε: ↑
Κυρ Μαρ 22, 2020 7:00 pm

Πρόβλημα 5: Να υπολογιστεί το ολοκλήρωμα $\int_{0}^{\frac{\pi}{4}}arctan(\sqrt{\frac{1}{2}(1-tan^{2}x)})dx$

Δύσκολο!

$\displaystyle{\begin{aligned} \int_{0}^{\pi/4} \arctan \sqrt{\frac{1-\tan^2 t}{2}}\, \mathrm{d}t &\overset{1-\tan^2 t \mapsto 2t^2}{=\! =\! =\! =\! =\! =\!=\!=\!} \int_{0}^{\sqrt{2}/2} \frac{t \arctan t}{\sqrt{1-2t^2} \left ( 1-t^2 \right )} \, \mathrm{d}t \\ &=\cancelto{0}{\left [ - \arctan \sqrt{1-2t^2} \arctan t \right ]_0^{\sqrt{2}/2}} + \int_{0}^{\sqrt{2}/2} \frac{\arctan \sqrt{1-2t^2}}{1+t^2} \, \mathrm{d}t \end{aligned}}$
Φτάνω μέχρι εδώ, αλλά κωλύομαι! Καμία υπόδειξη;

Έχω στο νου μου το DUTIS ότι μάλλον θα χρειαστεί, αλλά πού θα εισάγω τη παράμετρο για τη παραγώγιση;

Φαίνεται ότι κάνει $\frac{\pi^2}{24}$ . Απόδειξη ;

#10

Summand έγραψε: ↑
Κυρ Μαρ 22, 2020 7:00 pm
Β΄ Κατηγορία

Πρόβλημα 6: Να αποδειχτεί ότι για κάθε θετικό ακέραιο $n\geq 3$ υπάρχουν διακριτά σημεία στο επίπεδο, όχι συνευθειακά, ώστε όλες οι ανά δύο αποστάσεις μεταξύ των σημείων αυτών είναι ακέραιοι αριθμοί.

Ας το δυσκολέψουμε. Δείξτε το ίδιο με την επιπλέον συνθήκη ότι τα σημεία πρέπει να είναι ανά τρία μη συνευθειακά.

#11

Demetres έγραψε: ↑
Τετ Μαρ 25, 2020 11:44 am

Summand έγραψε: ↑
Κυρ Μαρ 22, 2020 7:00 pm
Β΄ Κατηγορία

Πρόβλημα 6: Να αποδειχτεί ότι για κάθε θετικό ακέραιο $n\geq 3$ υπάρχουν διακριτά σημεία στο επίπεδο, όχι συνευθειακά, ώστε όλες οι ανά δύο αποστάσεις μεταξύ των σημείων αυτών είναι ακέραιοι αριθμοί.

Ας το δυσκολέψουμε. Δείξτε το ίδιο με την επιπλέον συνθήκη ότι τα σημεία πρέπει να είναι ανά τρία μη συνευθειακά.

Να το δυσκολέψουμε και άλλο: Να βρείτε σημεία σε κύκλο.

(Αρχικά αυτό το τελευταίο είχα δείξει, αλλά έγραψα την παραπάνω λύση ως ευκολότερη. Πάντως το πέρασμα από την λύση που έγραψα (τα σημεία είναι σχεδόν όλα σε ευθεία) σε κύκλο είναι σχεδόν άμεσο αν το δεις σωστά (με κολπάκι).

#12

Summand έγραψε: ↑
Κυρ Μαρ 22, 2020 7:00 pm

Α΄ Κατηγορία

Πρόβλημα 6: Είναι δυνατό στον Ευκλείδειο χώρο $\mathbb{R}^{2}$ ένα αριθμήσιμο σύνολο μεμονωμένων σημείων να έχει μη υπεραριθμήσιμα συσσώρευσης;

Ναι υπάρχει. Έστω $q_1,q_2,\ldots$ μια απαρίθμηση των ρητών και έστω $\mathbb{N} = A_1 \cup A_2 \cup \cdots$ όπου $Α_1,A_2,\ldots$ ξένα μεταξύ τους απειροσύνολα. (Υπάρχει τέτοια γραφή αφού υπάρχει και 1-1 και επί συνάρτηση $f:\mathbb{N} \to \mathbb{N}^2$ .)

Θεωρούμε τώρα τα σημεία $\{(q_k,1/2^m):k \in \mathbb{N}, m\in A_k\}$ . Κάθε σημείο είναι μεμονωμένο. Πράγματι για κάθε $n \in \mathbb{N}$ υπάρχει μοναδικό της μορφής (q,1/2^n)

και αυτό ανήκει σε ένα ανοικτό δίσκο ακτίνας $1/2^{n+1}$ το οποίο δεν περιέχει κανένα άλλο από τα σημεία. Επίσης κάθε σημείο της μορφής (r,0)

με $r \in \mathbb{R}$ είναι σημείο συσσώρευσης. Πράγματι για $\delta > 0$ παίρνουμε $q \in \mathbb{Q}$ με $|r-q| < \delta/2$ . Αν q= q_k

παίρνουμε και $m \in A_k$ με $1/2^m < \delta/2$ . (Υπάρχει διότι A_k

απειροσύνολο.) Τότε $\|(r,0) - (q,1/2^m)\| < \delta$ .

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #13

Demetres έγραψε: ↑
Τετ Μαρ 25, 2020 12:02 pm

Summand έγραψε: ↑
Κυρ Μαρ 22, 2020 7:00 pm

Α΄ Κατηγορία

Πρόβλημα 6: Είναι δυνατό στον Ευκλείδειο χώρο $\mathbb{R}^{2}$ ένα αριθμήσιμο σύνολο μεμονωμένων σημείων να έχει μη υπεραριθμήσιμα συσσώρευσης;

Ναι υπάρχει. Έστω $q_1,q_2,\ldots$ μια απαρίθμηση των ρητών και έστω $\mathbb{N} = A_1 \cup A_2 \cup \cdots$ όπου $Α_1,A_2,\ldots$ ξένα μεταξύ τους απειροσύνολα. (Υπάρχει τέτοια γραφή αφού υπάρχει και 1-1 και επί συνάρτηση $f:\mathbb{N} \to \mathbb{N}^2$ .)

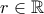Θεωρούμε τώρα τα σημεία $\{(q_k,1/2^m):k \in \mathbb{N}, m\in A_k\}$ . Κάθε σημείο είναι μεμονωμένο. Πράγματι για κάθε $n \in \mathbb{N}$ υπάρχει μοναδικό της μορφής και αυτό ανήκει σε ένα ανοικτό δίσκο ακτίνας $1/2^{n+1}$ το οποίο δεν περιέχει κανένα άλλο από τα σημεία. Επίσης κάθε σημείο της μορφής με $r \in \mathbb{R}$ είναι σημείο συσσώρευσης. Πράγματι για $\delta > 0$ παίρνουμε $q \in \mathbb{Q}$ με $|r-q| < \delta/2$ . Αν παίρνουμε και $m \in A_k$ με $1/2^m < \delta/2$ . (Υπάρχει διότι απειροσύνολο.) Τότε $\|(r,0) - (q,1/2^m)\| < \delta$ .

Υπάρχει ασάφεια στην εκφώνηση.
Θα έπρεπε να είναι

Είναι δυνατό στον Ευκλείδειο χώρο $\mathbb{R}^{2}$ ένα αριθμήσιμο σύνολο μεμονωμένων σημείων να έχει υπεραριθμήσιμο σύνολο σημείων συσσώρευσης;

Ως προς την λύση μπορούμε να πάρουμε το
$\left \{ (q_{n},\frac{1}{(p_{n})^{k}}):n,k=1,2,.... \right \}$
Οπου $q_{n},n=1,2,...$
αρίθμηση των ρητών
και $p_{n},n=1,2,...$
οι πρώτοι αριθμοί.
Την απόδειξη την έχει κάνει ο Δημήτρης.

Λάμπρος Κατσάπας · #14

ChrP έγραψε: ↑
Κυρ Μαρ 22, 2020 9:26 pm

Έστω $f(x_{n-1})=x_{n}$ με $f(x)=\frac{x}{x^2+x+1}$ τότε $f'(x)= \frac{x^2+x+1-x(2x+1)}{(x^2+x+1)^2}$ αρα $|f΄(x)|=|\frac{1-x^2}{(x^2+x+1)^2} |\leq 1$ (Η τελευταία ανισότητα προκύπτει από $|1-x^2| \leq |(x^2+x+1)^2 |$ , .Άρα η f είναι συστολή Lipchitz και είναι γνωστό ότι η f έχει μοναδικό σταθερό σημείο $f(l)=\lim_{n\to \infty}f(x_n)= \lim_{n\to \infty}x_n=l$ (Banach fixed point theorem )
Αρα τελικά συγγλινει .βάζοντας όρια στην σχέση έχουμε $l=\frac{l}{l^2+l+1}$ που δίνει η το οποίο απορρίπτεται αφού θετική με επαγωγή

Ποιο απλά, χωρίς βαρύ θεώρημα, η (x_n)

είναι γνησίως φθίνουσα.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #15

ChrP έγραψε: ↑
Κυρ Μαρ 22, 2020 9:26 pm

Πρόβλημα 2: Έστω ${x_{n}}$ ακολουθία τέτοια ώστε και $x_n=\frac{x_{n-1}}{x_{n-1}^{2}+x_{n-1}+1}, n\geq 1$ . Αποδείξτε ότι η ακολουθία ${nx_{n}}$ συγκλίνει και βρείτε το όριο της
Έστω $f(x_{n-1})=x_{n}$ με $f(x)=\frac{x}{x^2+x+1}$ τότε $f'(x)= \frac{x^2+x+1-x(2x+1)}{(x^2+x+1)^2}$ αρα $|f΄(x)|=|\frac{1-x^2}{(x^2+x+1)^2} |\leq 1$ (Η τελευταία ανισότητα προκύπτει από $|1-x^2| \leq |(x^2+x+1)^2 |$ , .Άρα η f είναι συστολή Lipchitz και είναι γνωστό ότι η f έχει μοναδικό σταθερό σημείο $f(l)=\lim_{n\to \infty}f(x_n)= \lim_{n\to \infty}x_n=l$ (Banach fixed point theorem )
Αρα τελικά συγγλινει .βάζοντας όρια στην σχέση έχουμε $l=\frac{l}{l^2+l+1}$ που δίνει η το οποίο απορρίπτεται αφού θετική με επαγωγή
Τώρα αντί για την θα μελετήσουμε την $\frac{1}{nx_n}$
$\frac{1}{nx_n}=\frac{\frac{1}{x_n}}{n}$
Από λήμμα stolz-cesaro το ζητούμενο όριο θα είναι ίσο με το $\frac{1}{x_{n+1}}-\frac{1}{x_n}= =\frac{x_{n}^{2}+x_{n}+1}{x_n}- \frac{1}{x_n}=x_n+1 \rightarrow 1$
Άρα τελικά $nx_n \rightarrow 1$

Δεν μπορεί να εφαρμοσθεί Banach fixed point theorem .
Για να είναι συστολή πρέπει
$|f΄(x)| \leq c< 1$
Εδω επειδή συγκλίνει στο

και

αποκλείεται να βρούμε διάστημα για να
εφαρμόσουμε το Banach fixed point theorem

Tolaso J Kos · #16

Tolaso J Kos έγραψε: ↑
Δευ Μαρ 23, 2020 1:08 am

Summand έγραψε: ↑
Κυρ Μαρ 22, 2020 7:00 pm

Πρόβλημα 5: Να υπολογιστεί το ολοκλήρωμα $\int_{0}^{\frac{\pi}{4}}arctan(\sqrt{\frac{1}{2}(1-tan^{2}x)})dx$

Δύσκολο!

$\displaystyle{\begin{aligned} \int_{0}^{\pi/4} \arctan \sqrt{\frac{1-\tan^2 t}{2}}\, \mathrm{d}t &\overset{1-\tan^2 t \mapsto 2t^2}{=\! =\! =\! =\! =\! =\!=\!=\!} \int_{0}^{\sqrt{2}/2} \frac{t \arctan t}{\sqrt{1-2t^2} \left ( 1-t^2 \right )} \, \mathrm{d}t \\ &=\cancelto{0}{\left [ - \arctan \sqrt{1-2t^2} \arctan t \right ]_0^{\sqrt{2}/2}} + \int_{0}^{\sqrt{2}/2} \frac{\arctan \sqrt{1-2t^2}}{1+t^2} \, \mathrm{d}t \end{aligned}}$

Συνεχίζω από δω.

$\displaystyle{\begin{aligned} \int_{0}^{\sqrt{2}/2} \frac{\arctan \sqrt{1-2t^2}}{1+t^2} \, \mathrm{d}t &= \int_{0}^{1} \frac{1}{1+x^2} \arctan \sqrt{\frac{1-x^2}{2}} \, \mathrm{d}x \\ &=-\sqrt{2} \int_{0}^{1} \frac{x \arctan x}{\sqrt{1-x^2} \left ( 3-x^2 \right )} \, \mathrm{d}x\\ &=-\sqrt{2} \int_{0}^{1}\frac{x}{\sqrt{1-x^2}\left ( 3-x^2 \right )} \int_{0}^{1} \frac{x}{1+x^2t^2} \, \mathrm{d}t \, \mathrm{d}x \\ &= -\sqrt{2} \int_{0}^{1} \int_{0}^{1} \frac{x^2}{\sqrt{1-x^2}\left ( 3-x^2 \right ) \left ( x^2+ \frac{1}{t^2} \right )} \frac{1}{t^2} \, \mathrm{d}x \, \mathrm{d}t\\ &\!\!\!\!\!\overset{x=\cos \theta}{=\! =\! =\! =\!} \sqrt{2} \int_{0}^{1} \int_{0}^{\pi/2} \frac{\cos^2 \theta}{\left ( 3 - \cos^2 \theta \right )\left ( \cos^2 \theta + \frac{1}{t^2} \right )} \, \mathrm{d}\theta \; \frac{\mathrm{d}t}{t^2} \\ &= \frac{\sqrt{2}}{3} \int_{0}^{1} \int_{0}^{\pi/2} \frac{\sec^2 \theta}{\left ( \sec^2 \theta - \frac{1}{3} \right ) \left ( t^2 + \sec^2 \theta \right )} \, \mathrm{d} \theta \, \mathrm{d}t \\ &=\frac{\sqrt{2}}{3} \int_{0}^{1} \int_{0}^{\pi/2} \frac{\sec^2 \theta}{\left ( \tan^2 \theta + \frac{2}{3} \right )\left ( \tan^2 \theta + 1 + t^2 \right )} \, \mathrm{d}\theta \, \mathrm{d}t \\ &=\frac{\sqrt{2}}{3} \bigintsss_{0}^{1} \left ( \int_{0}^{\pi/2} \frac{\sec^2 \theta}{\tan^2 \theta + \frac{2}{3}} \, \mathrm{d} \theta - \int_{0}^{\pi/2} \frac{\sec^2 \theta}{\tan^2 \theta + 1 + t^2} \, \mathrm{d}\theta \right ) \frac{\mathrm{d}t}{t^2+\frac{1}{3}} \end{aligned}}$
Κάπως καλύτερα , τώρα. Για τα δύο ολοκληρώματα που έχουν μείνει έχουμε:

$\displaystyle{\begin{aligned} \int_{0}^{\pi/2} \frac{\sec^2 \theta}{\tan^2 \theta + \frac{2}{3}} \, \mathrm{d}\theta &\overset{u =\tan \theta}{=\! =\! =\! =\!} \int_{0}^{\infty} \frac{\mathrm{d}u}{u^2 + \frac{2}{3}} \\ &=\left [ \frac{\sqrt{3}}{2} \arctan \sqrt{\frac{3}{2}}u \right ]_0^\infty \\ &= \frac{\sqrt{3}\pi}{2\sqrt{2}} \\ &= \frac{\pi \sqrt{6}}{4} \end{aligned}}$
Παρόμοιο το άλλο υπολογίζεται σε

$\displaystyle{\int_{0}^{\pi/2} \frac{\sec^2 \theta}{\tan^2 \theta + 1 + t^2} \, \mathrm{d}\theta = \frac{\pi}{2 \sqrt{1+t^2}}}$
Τότε,

$\displaystyle{\begin{aligned} \int_{0}^{1} \left ( \int_{0}^{\pi/2} \frac{\sec^2 \theta}{\tan^2 \theta + \frac{2}{3}} \, \mathrm{d} \theta - \int_{0}^{\pi/2} \frac{\sec^2 \theta}{\tan^2 \theta + 1 + t^2} \, \mathrm{d}\theta \right ) \frac{\mathrm{d}t}{t^2+\frac{1}{3}} &= \frac{\pi \sqrt{6}}{4}\int_{0}^{1} \frac{\mathrm{d}t}{t^2 + \frac{1}{3}} - \frac{\pi}{2}\int_{0}^{1} \frac{\mathrm{d}t}{\sqrt{1+t^2} \left ( t^2 + \frac{1}{3} \right )} \\ &\!\!\!\!\!\overset{t \mapsto 1/t}{=\! =\! =\! =\! =\!}\frac{\pi \sqrt{6}}{4} \frac{\pi}{\sqrt{3}} - \frac{3 \pi}{2} \int_{1}^{\infty} \frac{t}{\sqrt{t^2+1} \left ( t^2+3 \right )} \, \mathrm{d}t \\ &\!\!\!\!\!\!\overset{t \mapsto t^2}{=\! =\! =\! =\!} \frac{\pi^2 \sqrt{2}}{4} - \frac{3\pi}{4} \int_{1}^{\infty} \frac{\mathrm{d}t}{\sqrt{t+1} (t+3)} \\ &=\frac{\pi^2 \sqrt{2}}{4} - \frac{3\pi}{4}\int_{2}^{\infty} \frac{\mathrm{d}t}{\sqrt{t} \left ( t+2 \right )} \\ &\!\!\!\!\!\overset{t \mapsto t^2}{=\! =\! =\! =\!} \frac{\pi^2 \sqrt{2}}{4} - \frac{3\pi}{2} \int_{\sqrt{2}}^{\infty} \frac{\mathrm{d}t}{t^2+2} \\ &= \frac{\pi^2 \sqrt{2}}{4} - \frac{3\pi^2}{8\sqrt{2}} \end{aligned}}$
Μαζεύοντας , έχουμε:

$\displaystyle{\begin{aligned} \int_{0}^{\pi/4} \arctan \sqrt{\frac{1-\tan^2 \theta}{2}} \, \mathrm{d}\theta &= \frac{\sqrt{2}}{3} \left ( \frac{\pi^2 \sqrt{2}}{4} - \frac{3\sqrt{2} \pi^2}{16} \right ) \\ &= \frac{\sqrt{2}}{3} \cdot \frac{\sqrt{2}\pi^2}{16}\\ &= \frac{\pi^2}{24} \end{aligned}}$

Πάρα πολύ δύσκολο για διαγωνισμό.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #17

Summand έγραψε: ↑
Κυρ Μαρ 22, 2020 7:00 pm

Πρόβλημα 2: Έστω ${a_{n}}$ ακολουθία τέτοια ώστε $a_{0}=1, a_{1}=2, a_{n+1}=\frac{3^{n-1}+a_{n}^{2}}{a_{n-1}},n\geq 1$
a) Δείξτε ότι οι αριθμοί $a_{n}$ είναι ακέραιοι.
b) Συγκλίνει η σειρά $\sum_{n=0}^{\infty }\frac{1}{a_{n}}$ ;
c) Συγκλίνει η σειρά $\sum_{n=0}^{\infty }\frac{a_{n+1}}{a_{n}}$ ;

Φιλικά,
Γιάννης

Γράφουμε κάτω μερικούς όρους της ακολουθίας και παρατηρούμε !!!!!!!!!!!!!
ότι
$a_{n+1}=a_{n}+3^{n}$
Αμεσο είναι ότι
$a_{n}=1+\dfrac{3^{n}-1}{2}$
(το αποδεικνύουμε επαγωγικά)
και όλα είναι τετριμμένα.

#18

Tolaso J Kos έγραψε: ↑
Τετ Μαρ 25, 2020 11:50 pm
... Πάρα πολύ δύσκολο για διαγωνισμό.

Το ολοκλήρωμα είναι πράγματι πολύ δύσκολο, ακόμα κι αν η μοναδική επίλυση αναγκαστικά "περνάει" από όσα χρησιμοποίησες παραπάνω. Δυστυχώς, από ότι βλέπω οι διοργανωτές δεν έχουν ανεβάσει λύσεις των θεμάτων -έως σήμερα- ώστε να δούμε και την επίλυση του ολοκληρώματος.

#19

Summand έγραψε: ↑
Κυρ Μαρ 22, 2020 7:00 pm
Α΄ Κατηγορία

Πρόβλημα 1: Μυρμήγκια κάθονται σε κάθε μια από τις κορυφές $A_i \ (i=1,2,...,n)$ και στο κέντρο ενός κανονικού ν-γώνου. Τα μυρμήγκια ξεκινούν να κινούνται κατά μήκος των πλευρών του ν-γώνου και κατά μήκος των γραμμών $A_iO \ (i=1,2,...,n)$ . Υπολογίστε την πιθανότητα να μη συναντηθούν τα μυρμήγκια.

Κάπως ασαφές. Φαντάζομαι εννοεί ότι κάνουν από μία κίνηση από εκεί που βρίσκονται σε μια γειτονική κορυφή (ή στο κέντρο) και ότι απαγορεύεται να συναντηθούν και στο τέλος της διαδρομής τους (στην ίδια π.χ. κορυφή) και κατά τη διάρκεια της διαδρομής τους (π.χ. κινούμενα στην ίδια ακμή).

Κατασκευάζουμε ένα κατευθυνόμενο γράφημα

με κορυφές τα $O,A_1,\ldots,A_n$ και ακμή από μια κορυφή

σε μια άλλη κορυφή

αν το μυρμήγκι κινηθεί από τη

στη

. Σε αυτό το γράφημα από κάθε κορυφή φεύγει μια κετευθυνόμενη ακμή αλλά και καταλήγει μια κατευθυνόμενη ακμή αφού τα μυρμήγκια πρέπει να καταλήξουν σε διαφορετικές κορύφες. Άρα το

είναι ένωση κύκλων. Ας παρατηρήσουμε ότι αν σβήσουμε την

και μια οποιαδήποτε άλλη κορυφή δεν μπορούμε να έχουμε κύκλο στις υπόλοιπες κορυφές. Επειδή το μυρμήγκι στην

πάει σε κάποια άλλη κορυφή θα υπάρχει ακριβώς ένας κύκλος που θα περιέχει όλες τις κορυφές. Έχουμε

επιλογές για το που θα πάει το μυρμήγκι στο

, έστω ότι πάει στο A_i

. Έχουμε επίσης

επιλογές για το που θα πάει το μυρμήγκι του A_i

. Ακολούθως όλες οι υπόλοιπες κινήσεις καθορίζονται πλήρως.

Άρα υπάρχουν

τρόποι να κινηθούν τα μυρμήγκια χωρίς να συναντηθούν. Επίσης υπάρχουν n3^n

να κινηθούν τα μυρμήγκια χωρίς περιορισμούς. Άρα έχουμε πιθανότητα 2/3^n

να μην συναντηθούν.

Tolaso J Kos · #20

grigkost έγραψε: ↑
Πέμ Μαρ 26, 2020 6:34 pm

Tolaso J Kos έγραψε: ↑
Τετ Μαρ 25, 2020 11:50 pm
... Πάρα πολύ δύσκολο για διαγωνισμό.
Το ολοκλήρωμα είναι πράγματι πολύ δύσκολο, ακόμα κι αν η μοναδική επίλυση αναγκαστικά "περνάει" από όσα χρησιμοποίησες παραπάνω. Δυστυχώς, από ότι βλέπω οι διοργανωτές δεν έχουν ανεβάσει λύσεις των θεμάτων -έως σήμερα- ώστε να δούμε και την επίλυση του ολοκληρώματος.

Δε πιστεύω ότι είναι μοναδική. Σίγουρα θα λειτουργεί και κάποια μέθοδος με σειρά , ανάπτυγμα με $\arctan$ . Δε πιστεύω όμως ότι θα 'ναι εύκολη. Αν κρίνω από το τι θα πρέπει να ολοκληρωθεί η σειρά μάλλον θα περιέχει διωνυμικά. Η παραπάνω λύση χρησιμοποιεί το απλό γεγονός

$\displaystyle{\arctan x = \int_0^1 \frac{x}{1+t^2 x^2} \, \mathrm{d}t}$
το οποίο είναι γνωστό τέχνασμα , αλλά το διπλό ολοκλήρωμα δε το χειρίζεσαι εύκολα. Μου θυμίζει έντονα την οικογένεια ολοκληρωμάτων Ahmed και αυτό πρέπει να εμπίπτει εκεί. Αυτά τα ολοκληρώματα είναι γνωστά εδώ και χρόνια όπως επίσης τα πιο παρεμφερή της οικογένειας Coxeter. Ένα έχουμε δει εδώ πριν πολλά χρόνια.

Επισυνάπτω ένα αρχείο του sos440 όπου έχει μελετήσει τη γενικότερη μορφή των Ahmed.

doc_026_Ahmed_Integral.pdf: (102.79 KiB) Μεταφορτώθηκε 30 φορές

3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Re: 3η Ανοιχτή Μαθηματική Ολυμπιάδα για φοιτητές

Μέλη σε σύνδεση