sot arm έγραψε: ↑Κυρ Ιαν 27, 2019 9:09 pm
Πρόβλημα 5:
Θεωρούμε

πίνακες

με στοιχεία ακέραιους αριθμούς, τέτοιους ώστε

και

, και θέτουμε

. Δείξτε ότι υπάρχει θετικός ακέραιος k
για τον οποίο όλα τα στοιχεία του πίνακα

είναι ακέραιοι αριθμοί.
Έστω
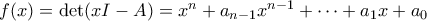
το χαρακτηριστικό πολυώνυμο του

. Το

έχει ακέραιους συντελεστές.
Λήμμα: Για κάθε θετικό ακέραιο

μπορούμε να γράψουμε

όπου οι ακολουθίες ακεραίων
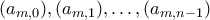
ικανοποιούν την αναδρομική σχέση

μαζί με τις αρχικές συνθήκες

και

για

με

.
Απόδειξη λήμματος: Θα το δείξουμε με ισχυρή επαγωγή. Ο ισχυρισμός είναι άμεσος για

. Έστω λοιπόν ότι ισχύει για

. Θα δείξουμε ότι ισχύει και για

.
Επειδή

έχουμε

άρα και

. Άρα από την επαγωγική υπόθεση

όπου

Δηλαδή ο ισχυρισμός ισχύει και για

.

Κοιτάμε τώρα κάθε μία από τις ακολουθίες

modulo

. (Αγνοούμε την

.) Κάθε μια από αυτές ικανοποιεί την αναδρομική σχέση

οπότε είναι περιοδική. (
Δείτε στην τελευταία παράγραφο γιατί.) Έστω ότι η

είναι περιοδική με περίοδο

. Τότε θα έχουμε

για κάθε

πολλαπλάσιο του

. Θέτουμε

και παρατηρούμε ότι

για κάθε

.
Από το λήμμα έχουμε

άρα και

Ο πίνακας

έχει ακέραια στοιχεία επειδή το ίδιο ισχύει για κάθε ένα από τους

. Για

όλα τα στοιχεία είναι πολλαπλάσια του

. Το ίδιο όμως ισχύει και για
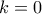
αφού ο πίνακας θα είναι ο

.
Άρα όλα τα στοιχεία του

είναι ακέραια πολλαπλάσια του

και άρα όλα τα στοιχεία του

είναι ακέραια.
Σημείωση: Δεν χρησιμοποιήσαμε πουθενά το γεγονός ότι  .
Προσθήκη αργότερα:
.
Προσθήκη αργότερα: Όπως με ενημέρωσε με π.μ. ο Αντώνης Ζητρίδης, χρειάζεται τελικά το

για να δείξω ότι η αναδρομική σχέση δίνει περιοδική ακολουθία.
Έστω λοιπόν ότι έχω μια αναδρομική ακολουθία που ικανοποιεί την σχέση

modulo κάποιον φυσικό

. Από περιστερώνα θα υπάρχουν δύο υπακολουθίες

συνεχόμενων όρων οι οποίες θα είναι ακριβώς οι ίδιες. Δηλαδή θα υπάρχουν

ώστε

. Επαγωγικά είναι απλό ότι

για κάθε φυσικό

. Για να δείξουμε όμως

για κάθε φυσικό

πρέπει να μπορούμε να πάμε και προς τα πίσω. Για να γίνει αυτό πρέπει να μπορούμε να λύσουμε την αναδρομική σχέση ως προς

. Αυτό γίνεται αν το

είναι αντιστρέψιμο modulo

διότι τότε θα έχουμε

. Στην περίπτωσή μας, λόγω του

ο συγκεκριμένος συντελεστής ισούται με

ή

οπότε παίρνουμε την περιοδικότητα της ακολουθίας.
 να είναι ρητός αριθμός.
να είναι ρητός αριθμός. το σύνολο των
το σύνολο των  πινάκων
πινάκων  με στοιχεία πραγματικούς αριθμούς με την εξής ιδιότητα: υπάρχει μη μηδενικό πολυώνυμο
με στοιχεία πραγματικούς αριθμούς με την εξής ιδιότητα: υπάρχει μη μηδενικό πολυώνυμο  με μη αρνητικούς πραγματικούς συντελεστές έτσι ώστε
με μη αρνητικούς πραγματικούς συντελεστές έτσι ώστε  .Έστω επίσης
.Έστω επίσης  το σύνολο των συμμετρικών
το σύνολο των συμμετρικών  πινάκων.Για ποιους ακέραιους ν ισχύει:
πινάκων.Για ποιους ακέραιους ν ισχύει: ;
;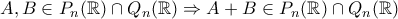
 με
με  .Για ποιά
.Για ποιά  υπάρχει συνεχής, αύξουσα συνάρτηση
υπάρχει συνεχής, αύξουσα συνάρτηση ![\displaystyle{f:[a,b] \rightarrow [0,+\infty)} \displaystyle{f:[a,b] \rightarrow [0,+\infty)}](/forum/ext/geomar/texintegr/latexrender/pictures/469c7f223f6459c83cee0b22f3e78264.png) , όχι ταυτοτικά μηδέν, έτσι ώστε:
, όχι ταυτοτικά μηδέν, έτσι ώστε: ;
;  υπάρχει
υπάρχει  πίνακας
πίνακας  με στοιχεία ρητούς έτσι ώστε:
με στοιχεία ρητούς έτσι ώστε: Πρόβλημα 5:
Πρόβλημα 5: πίνακες
πίνακες  με στοιχεία ακέραιους αριθμούς, τέτοιους ώστε
με στοιχεία ακέραιους αριθμούς, τέτοιους ώστε και
και  , και θέτουμε
, και θέτουμε  . Δείξτε ότι υπάρχει θετικός ακέραιος k
. Δείξτε ότι υπάρχει θετικός ακέραιος k







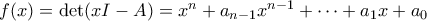 το χαρακτηριστικό πολυώνυμο του
το χαρακτηριστικό πολυώνυμο του  . Το
. Το  έχει ακέραιους συντελεστές.
έχει ακέραιους συντελεστές. μπορούμε να γράψουμε
μπορούμε να γράψουμε 
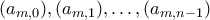 ικανοποιούν την αναδρομική σχέση
ικανοποιούν την αναδρομική σχέση
 και
και  για
για  με
με  .
. . Έστω λοιπόν ότι ισχύει για
. Έστω λοιπόν ότι ισχύει για  . Θα δείξουμε ότι ισχύει και για
. Θα δείξουμε ότι ισχύει και για  .
. έχουμε
έχουμε  άρα και
άρα και  . Άρα από την επαγωγική υπόθεση
. Άρα από την επαγωγική υπόθεση


 modulo
modulo  . (Αγνοούμε την
. (Αγνοούμε την  .) Κάθε μια από αυτές ικανοποιεί την αναδρομική σχέση
.) Κάθε μια από αυτές ικανοποιεί την αναδρομική σχέση  οπότε είναι περιοδική. (
οπότε είναι περιοδική. ( είναι περιοδική με περίοδο
είναι περιοδική με περίοδο  . Τότε θα έχουμε
. Τότε θα έχουμε  για κάθε
για κάθε  και παρατηρούμε ότι
και παρατηρούμε ότι  για κάθε
για κάθε  .
.

 έχει ακέραια στοιχεία επειδή το ίδιο ισχύει για κάθε ένα από τους
έχει ακέραια στοιχεία επειδή το ίδιο ισχύει για κάθε ένα από τους  . Για
. Για  όλα τα στοιχεία είναι πολλαπλάσια του
όλα τα στοιχεία είναι πολλαπλάσια του 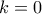 αφού ο πίνακας θα είναι ο
αφού ο πίνακας θα είναι ο  .
. είναι ακέραια πολλαπλάσια του
είναι ακέραια πολλαπλάσια του  είναι ακέραια.
είναι ακέραια. .
. modulo κάποιον φυσικό
modulo κάποιον φυσικό  . Από περιστερώνα θα υπάρχουν δύο υπακολουθίες
. Από περιστερώνα θα υπάρχουν δύο υπακολουθίες  συνεχόμενων όρων οι οποίες θα είναι ακριβώς οι ίδιες. Δηλαδή θα υπάρχουν
συνεχόμενων όρων οι οποίες θα είναι ακριβώς οι ίδιες. Δηλαδή θα υπάρχουν  ώστε
ώστε  . Επαγωγικά είναι απλό ότι
. Επαγωγικά είναι απλό ότι  για κάθε φυσικό
για κάθε φυσικό  για κάθε φυσικό
για κάθε φυσικό  πρέπει να μπορούμε να πάμε και προς τα πίσω. Για να γίνει αυτό πρέπει να μπορούμε να λύσουμε την αναδρομική σχέση ως προς
πρέπει να μπορούμε να πάμε και προς τα πίσω. Για να γίνει αυτό πρέπει να μπορούμε να λύσουμε την αναδρομική σχέση ως προς  . Αυτό γίνεται αν το
. Αυτό γίνεται αν το  είναι αντιστρέψιμο modulo
είναι αντιστρέψιμο modulo  . Στην περίπτωσή μας, λόγω του
. Στην περίπτωσή μας, λόγω του  ή
ή  οπότε παίρνουμε την περιοδικότητα της ακολουθίας.
οπότε παίρνουμε την περιοδικότητα της ακολουθίας. (1)
(1) είναι αύξουσα από γνωστή ανισότητα έχουμε
είναι αύξουσα από γνωστή ανισότητα έχουμε 


 τότε δεν μπορεί να ανήκει στον
τότε δεν μπορεί να ανήκει στον  . Πράγματι, αν
. Πράγματι, αν  τότε το
τότε το  είναι πολλαπλάσιο του ελάχιστου πολυωνύμου
είναι πολλαπλάσιο του ελάχιστου πολυωνύμου  . Πρέπει
. Πρέπει  άρα και
άρα και  . Τότε όμως το
. Τότε όμως το  όπου
όπου  για κάθε
για κάθε  .
.  τότε πρέπει και
τότε πρέπει και  . Σε αντίθετη περίπτωση ο
. Σε αντίθετη περίπτωση ο 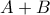 πρέπει να έχει τουλάχιστον μία θετική ιδιοτιμή
πρέπει να έχει τουλάχιστον μία θετική ιδιοτιμή  το αντίστοιχο ιδιοδιάνυσμα. Τότε
το αντίστοιχο ιδιοδιάνυσμα. Τότε  που δίνει ότι
που δίνει ότι  ή
ή  . Χωρίς βλάβη της γενικότητας είναι
. Χωρίς βλάβη της γενικότητας είναι  μια βάση ιδιοδιανυσμάτων του
μια βάση ιδιοδιανυσμάτων του  . (Υπάρχει επειδή
. (Υπάρχει επειδή  και παρατηρούμε ότι
και παρατηρούμε ότι  , άτοπο.
, άτοπο. .
. αφού
αφού  αν και μόνο αν
αν και μόνο αν  με
με  . Θα δείξουμε ότι δεν ισχύει για τα υπόλοιπα
. Θα δείξουμε ότι δεν ισχύει για τα υπόλοιπα  και
και 
 και
και  . Παρατηρούμε ότι
. Παρατηρούμε ότι  αφού μπορούμε να πάρουμε
αφού μπορούμε να πάρουμε  για τον
για τον  για τον
για τον  .
. ο οποίος έχει ως ιδιοτιμή το
ο οποίος έχει ως ιδιοτιμή το  .
. κατασκευάζοντας πίνακες που έχουν παντού μηδενικά εκτός από τις θέσεις του πάνω αριστερά
κατασκευάζοντας πίνακες που έχουν παντού μηδενικά εκτός από τις θέσεις του πάνω αριστερά  υποπίνακα όπου τοποθετούμε τους πίνακες του παραδείγματός μας.
υποπίνακα όπου τοποθετούμε τους πίνακες του παραδείγματός μας. . Είναι
. Είναι  ,
, ώστε
ώστε  (θα είναι
(θα είναι  ). Θα αποδείξουμε πως για κάθε
). Θα αποδείξουμε πως για κάθε  αυτής της μορφής υπάρχει τέτοιος πίνακας
αυτής της μορφής υπάρχει τέτοιος πίνακας  διαγωνοποιείται ως:
διαγωνοποιείται ως:
 .
.

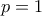 τώρα, μπορούμε να βρούμε και πάλι ιδιοδιανύσματα με ρητές συντεταγμένες για τον
τώρα, μπορούμε να βρούμε και πάλι ιδιοδιανύσματα με ρητές συντεταγμένες για τον  που αντιστοιχούν στις ιδιοτιμές
που αντιστοιχούν στις ιδιοτιμές  ,
,  , και
, και  , το
, το  ή το
ή το  είναι μια βάση γενικευμένων ιδιοδιανυσμάτων για τον
είναι μια βάση γενικευμένων ιδιοδιανυσμάτων για τον  είναι ιδιοτιμή (ένα απ' τα δύο).
είναι ιδιοτιμή (ένα απ' τα δύο).  ότι
ότι  όπου
όπου  και ο
και ο  υποθέτουμε χωρίς βλάβη
υποθέτουμε χωρίς βλάβη 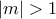
 πινάκων με στοιχεία από το
πινάκων με στοιχεία από το  , αφού
, αφού  . Αφού η ομάδα αυτή είναι πεπερασμένη, ο Α έχει πεπερασμένη τάξη, επομένως έπεται ότι υπάρχει ακέραιος
. Αφού η ομάδα αυτή είναι πεπερασμένη, ο Α έχει πεπερασμένη τάξη, επομένως έπεται ότι υπάρχει ακέραιος  τέτοιος ώστε:
τέτοιος ώστε: όπου ο
όπου ο  έχει ακέραια στοιχεία, το ζητούμενο έπεται.
έχει ακέραια στοιχεία, το ζητούμενο έπεται.