Ωραίο.
Θα το δείξω με επαγωγή στο

. Είναι προφανές όταν

αφού

, άρα
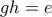
που δίνει

και άρα και

. Για το επαγωγικό βήμα ελέγχουμε δύο περιπτώσεις.
Περίπτωση 1: Αν

θέτω

. Τότε

για κάθε

. Θέτω

και

. Τότε

Από την επαγωγική υπόθεση έχουμε

. Δηλαδή

οπότε και

.
Περίπτωση 2: Αν

θέτω

. Θέτω

και

.
Επειδή

, κάθε

ισούται είτε με

είτε με

. Στη παράσταση

αντικαθιστώ κάθε εμφάνιση του

με

αν

και με

αν

για να πάρω μια παράσταση στα

η οποία είναι ίση με

.
Π.χ. για

έχουμε

. Η μετατροπή δίνει

που είναι ακριβώς η παράσταση που παίρνουμε για την περίπτωση

. Θέλουμε να δείξουμε ότι αυτό δεν είναι τυχαίο αλλά συμβαίνει πάντα. Είναι πιο δύσκολο από την πρώτη περίπτωση διότι τα

δεν σχετίζονται τόσο εύκολα με τα

.
Έστω ότι στο βήμα

έγραψα το

για

-οστή φορά. Αυτό σημαίνει ότι έγραψα και

φορές το

. Για να γράψω όμως τόσες φορές το

πρέπει ακριβώς

φορές να είχα

για

. Άρα

Επειδή

έχουμε επιπλέον ότι

Από το

παίρνουμε

που είναι ισοδύναμο με το

Από το

παίρνουμε

που είναι ισοδύναμο με το

Έχουμε λοιπόν ότι

Αυτό σημαίνει πως όταν γράψω το

-οστό

έχω γράψει ακριβώς

φορές το

. Δηλαδή

Εδώ πρέπει να δικαιολογήσω γιατί το

είναι ο τελευταίος όρος της παράστασης. Το πλήθος των

που γράφουμε είναι ίσο με

. Επίσης, το πλήθος των

είναι ίσο με

.
Από την επαγωγική υπόθεση έχουμε

. Δηλαδή

οπότε και

.
 και έστω
και έστω
 . Έστω
. Έστω  στοιχεία μιας ομάδας
στοιχεία μιας ομάδας  ώστε
ώστε
 το ταυτοτικό στοιχείο.
το ταυτοτικό στοιχείο.  .
. και έστω
και έστω
 . Έστω
. Έστω  στοιχεία μιας ομάδας
στοιχεία μιας ομάδας  ώστε
ώστε
 το ταυτοτικό στοιχείο.
το ταυτοτικό στοιχείο.  .
. . Είναι προφανές όταν
. Είναι προφανές όταν  αφού
αφού  , άρα
, άρα 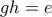 που δίνει
που δίνει  και άρα και
και άρα και  . Για το επαγωγικό βήμα ελέγχουμε δύο περιπτώσεις.
. Για το επαγωγικό βήμα ελέγχουμε δύο περιπτώσεις.  θέτω
θέτω  . Τότε
. Τότε  για κάθε
για κάθε  . Θέτω
. Θέτω  και
και  . Τότε
. Τότε
 . Δηλαδή
. Δηλαδή  οπότε και
οπότε και  .
.  θέτω
θέτω  . Θέτω
. Θέτω  και
και  .
. ισούται είτε με
ισούται είτε με  είτε με
είτε με  . Στη παράσταση
. Στη παράσταση  αντικαθιστώ κάθε εμφάνιση του
αντικαθιστώ κάθε εμφάνιση του  με
με  αν
αν  και με
και με  αν
αν  για να πάρω μια παράσταση στα
για να πάρω μια παράσταση στα  η οποία είναι ίση με
η οποία είναι ίση με  έχουμε
έχουμε  . Η μετατροπή δίνει
. Η μετατροπή δίνει  που είναι ακριβώς η παράσταση που παίρνουμε για την περίπτωση
που είναι ακριβώς η παράσταση που παίρνουμε για την περίπτωση  . Θέλουμε να δείξουμε ότι αυτό δεν είναι τυχαίο αλλά συμβαίνει πάντα. Είναι πιο δύσκολο από την πρώτη περίπτωση διότι τα
. Θέλουμε να δείξουμε ότι αυτό δεν είναι τυχαίο αλλά συμβαίνει πάντα. Είναι πιο δύσκολο από την πρώτη περίπτωση διότι τα  δεν σχετίζονται τόσο εύκολα με τα
δεν σχετίζονται τόσο εύκολα με τα  -οστή φορά. Αυτό σημαίνει ότι έγραψα και
-οστή φορά. Αυτό σημαίνει ότι έγραψα και  φορές το
φορές το  για
για  . Άρα
. Άρα  Επειδή
Επειδή 
 παίρνουμε
παίρνουμε  που είναι ισοδύναμο με το
που είναι ισοδύναμο με το 
 παίρνουμε
παίρνουμε  που είναι ισοδύναμο με το
που είναι ισοδύναμο με το 

 φορές το
φορές το 
 είναι ο τελευταίος όρος της παράστασης. Το πλήθος των
είναι ο τελευταίος όρος της παράστασης. Το πλήθος των  . Επίσης, το πλήθος των
. Επίσης, το πλήθος των  .
.  οπότε και
οπότε και