 τον αριθμό των bits του '1' στη δυική αναπαράσταση του
τον αριθμό των bits του '1' στη δυική αναπαράσταση του  . Υπολογίσατε τη σειρά
. Υπολογίσατε τη σειρά
Συντονιστής: Demetres
 . Το αντίστοιχο μερικό άθροισμα είναι
. Το αντίστοιχο μερικό άθροισμα είναι  .
. ή
ή  ως προς
ως προς  έχουν το ψηφίο των δυάδων
έχουν το ψηφίο των δυάδων  . Το αντίστοιχο μερικό άθροισμα είναι
. Το αντίστοιχο μερικό άθροισμα είναι 
 και ούτω καθεξής.
και ούτω καθεξής. 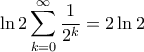
 που ορίζεται αναδρομικά ως
που ορίζεται αναδρομικά ως
 ,
,  μετράει τον αριθμό των
μετράει τον αριθμό των  στη δυική αναπαράσταση του
στη δυική αναπαράσταση του  . Τότε:
. Τότε:

 , θεωρούμε τη συνάρτηση
, θεωρούμε τη συνάρτηση

 αν-ν
αν-ν  για κάποιον
για κάποιον  . Συνεπώς,
. Συνεπώς, 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες