 ώστε ο πίνακας
ώστε ο πίνακας
να είναι το τετράγωνο ενός πίνακα με ρητά στοιχεία.
Επεξεργασία: Έγινε διόρθωση στην εκφώνηση.
Συντονιστής: Demetres
 ώστε ο πίνακας
ώστε ο πίνακας
 και
και  .
.  ισούται με
ισούται με  . Έτσι, οι ιδιοτιμές του είναι οι
. Έτσι, οι ιδιοτιμές του είναι οι 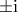 και ο
και ο  θα έχει ως ιδιοτιμή τουλάχιστον μία πρωτογενή όγδοη ρίζα της μονάδας, δηλαδή ρίζα του κυκλοτομικού πολυωνύμου
θα έχει ως ιδιοτιμή τουλάχιστον μία πρωτογενή όγδοη ρίζα της μονάδας, δηλαδή ρίζα του κυκλοτομικού πολυωνύμου  .
.  ) και έτσι, λόγω βαθμού, αυτό πρέπει να είναι το χαρακτηριστικό πολυώνυμο του
) και έτσι, λόγω βαθμού, αυτό πρέπει να είναι το χαρακτηριστικό πολυώνυμο του  . Έτσι, από το θεώρημα Cayley-Hamilton, πρέπει να ισχύει
. Έτσι, από το θεώρημα Cayley-Hamilton, πρέπει να ισχύει  .
.  και έτσι η μοναδική πιθανή λύση είναι
και έτσι η μοναδική πιθανή λύση είναι 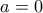 .
. , οπότε το
, οπότε το 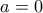 είναι λύση.
είναι λύση.
 αναγκαστικά θα είναι
αναγκαστικά θα είναι  .
. και
και  .
.
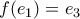 αναγκαστικά θα είναι
αναγκαστικά θα είναι  που προφανώς δεν οδηγεί σε πίνακα.
που προφανώς δεν οδηγεί σε πίνακα. αναγκαστικά θα είναι
αναγκαστικά θα είναι  .
. και
και  .
. τέτοιοι πίνακες με ακέραια στοιχεία.
τέτοιοι πίνακες με ακέραια στοιχεία.

 που είναι τετράγωνο του
που είναι τετράγωνο του  και έπραξα κατ' αναλογία...
και έπραξα κατ' αναλογία...Σωστά. Η εκφώνηση μιλούσε για ρητά στοιχεία. Απολογούμαι για το λάθος
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 22 επισκέπτες