 ώστε
ώστε
για κάθε
 . Να βρεθούν όλες οι δυνατές τιμές (πεπερασμένες ή άπειρες) του
. Να βρεθούν όλες οι δυνατές τιμές (πεπερασμένες ή άπειρες) του
Συντονιστής: Demetres
 ώστε
ώστε
 . Να βρεθούν όλες οι δυνατές τιμές (πεπερασμένες ή άπειρες) του
. Να βρεθούν όλες οι δυνατές τιμές (πεπερασμένες ή άπειρες) του
 ισχύει
ισχύει  , όπου
, όπου  .
. έχει ολικό ελάχιστο στο
έχει ολικό ελάχιστο στο  με τιμή
με τιμή  . Έτσι, για κάθε
. Έτσι, για κάθε  θα ισχύει ότι το
θα ισχύει ότι το  θα είναι είτε μεγαλύτερο ή ίσο του
θα είναι είτε μεγαλύτερο ή ίσο του  ("άνω κλάδος") είτε μικρότερο ή ίσο του
("άνω κλάδος") είτε μικρότερο ή ίσο του  ("κάτω κλάδος"). Αλλά το
("κάτω κλάδος"). Αλλά το  είναι διάστημα θετικού μέτρου. Έτσι, για να διασφαλιστεί η μονοτονία, πρέπει να επιλεγεί ο άνω κλάδος. Στο εξής θεωρούμε
είναι διάστημα θετικού μέτρου. Έτσι, για να διασφαλιστεί η μονοτονία, πρέπει να επιλεγεί ο άνω κλάδος. Στο εξής θεωρούμε  με πεδίο ορισμού
με πεδίο ορισμού  και
και  . Επομένως
. Επομένως  .
. είναι φραγμένο άνω, οπότε
είναι φραγμένο άνω, οπότε  . Αν
. Αν  , τότε
, τότε  (άτοπο). Επομένως
(άτοπο). Επομένως  και
και  .
.  . Το "πρέπει" είναι προφανές από τη μονοτονία. Για το "αρκεί", παρατηρούμε ότι, με τις κατάλληλες τιμές στο
. Το "πρέπει" είναι προφανές από τη μονοτονία. Για το "αρκεί", παρατηρούμε ότι, με τις κατάλληλες τιμές στο  (
(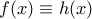 ), μπορούμε πάντα να κατασκευάσουμε γνησίως φθίνοντα τμήματα στο
), μπορούμε πάντα να κατασκευάσουμε γνησίως φθίνοντα τμήματα στο ![(- \infty, l] (- \infty, l]](/forum/ext/geomar/texintegr/latexrender/pictures/e4df1cc21a2db58c7badb77f2dff8827.png) (με τιμές στο
(με τιμές στο  ) και στο
) και στο  (με τιμές στο
(με τιμές στο ![(l, h(L)] (l, h(L)]](/forum/ext/geomar/texintegr/latexrender/pictures/3c5d2951b6cfad301195265cfa981cb9.png) ).
). , έπεται ότι
, έπεται ότι  (το μόνο σταθερό σημείο της φθίνουσας
(το μόνο σταθερό σημείο της φθίνουσας  ). Έτσι,
). Έτσι, ![L \in (1, 1 + 3 \cdot 4^{-4/3}] L \in (1, 1 + 3 \cdot 4^{-4/3}]](/forum/ext/geomar/texintegr/latexrender/pictures/b4b88db6a985e1050831cf3252646252.png) . Επιλέγοντας
. Επιλέγοντας  , επαληθεύουμε τη συνθήκη
, επαληθεύουμε τη συνθήκη  . Απομένει να επαληθευτεί η
. Απομένει να επαληθευτεί η  . Διαπιστώνουμε ότι
. Διαπιστώνουμε ότι  για κάθε
για κάθε ![x \in (1, 1 + 3 \cdot 4^{-4/3}] x \in (1, 1 + 3 \cdot 4^{-4/3}]](/forum/ext/geomar/texintegr/latexrender/pictures/a837a5c6d2f76df355694c8b1395a8af.png) (επειδή οι
(επειδή οι  είναι κοίλες,
είναι κοίλες,  και
και  . Αρκεί λοιπόν
. Αρκεί λοιπόν  .
. από το
από το ![(1, 1 + 3 \cdot 4^{-4/3}] (1, 1 + 3 \cdot 4^{-4/3}]](/forum/ext/geomar/texintegr/latexrender/pictures/e5d2e2c0afb95021c0ad9da864b400d5.png) , επιλέγοντας συγχρόνως το
, επιλέγοντας συγχρόνως το  από το
από το  . Αφού
. Αφού  και
και  , το
, το  ανήκει στο
ανήκει στο  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες