 ώστε
ώστε  και
και  .
. Αν
 , να δειχθεί ότι
, να δειχθεί ότι 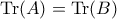 .
.Συντονιστής: Demetres
 , οι
, οι  είναι διαγωνιοποιήσιμοι. Επίσης, οι ιδιοτιμές του
είναι διαγωνιοποιήσιμοι. Επίσης, οι ιδιοτιμές του  είναι όλες
είναι όλες  -οστές ρίζες της μονάδας και, αφού το άθροισμά τους είναι
-οστές ρίζες της μονάδας και, αφού το άθροισμά τους είναι  , πρέπει να είναι όλες
, πρέπει να είναι όλες  . Λόγω του διαγωνιοποιήσιμου, έχουμε
. Λόγω του διαγωνιοποιήσιμου, έχουμε  .
.  του
του  (επίσης
(επίσης  -οστή ρίζα της μονάδας), η
-οστή ρίζα της μονάδας), η  θα είναι ιδιοτιμή του
θα είναι ιδιοτιμή του  (με την ίδια αλγεβρική πολλαπλότητα). Αλλά, αφού οι πίνακες είναι πραγματικοί, οι ιδιοτιμές είναι ζεύγη συζυγών. Οπότε τα αθροίσματά τους είναι ίσα και
(με την ίδια αλγεβρική πολλαπλότητα). Αλλά, αφού οι πίνακες είναι πραγματικοί, οι ιδιοτιμές είναι ζεύγη συζυγών. Οπότε τα αθροίσματά τους είναι ίσα και  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες