Να βάλω και εγώ το σκεπτικό μου.
Πρώτα υπέθεσα ότι η

είναι φραγμένη.Αυτό περιέχει και την περίπτωση να είναι αρνητική.
Τότε επειδή είναι γνησίως αύξουσα θα έχουμε

Eπειδή η παράγωγος είναι θετική και πάει να γλείψει ευθεία από κάτω θα είναι κοίλη.
Ετσι το

οπότε το ζητούμενο είναι προφανές.
(όταν έγραφα την λύση το είχα ξεχάσει και το έβαλα μετά)
Ετσι θεώρησα ότι το πρόβλημα έχει ενδιαφέρον όταν

Για να συνδέσω την

έφτιαξα μια ανισότητα μεταξύ των ολοκληρωμάτων.
Μετά είδα ότι η ανισότητα αυτή είναι στην ουσία η C-S.
Από την αρχή έκανα δυαδικό σπάσιμο γιατί γνωρίζω ότι αυτό είναι πολύ ισχυρό.
Τα υπόλοιπα τα βλέπετε παραπάνω.
Η απόδειξη του Δημήτρη έχει δύο διαφορές από την δική μου.
Η πρώτη είναι ότι δεν ξεχωρίζει περιπτώσεις.
Η δεύτερη είναι ότι δεν κάνει δυαδικό σπάσιμο.
Καλό είναι σε όλες τις λύσεις να μπαίνει το σκεπτικό.Το πρόβλημα τουλάχιστον για μένα είναι ότι πολλές φορές σκέφτομαι
ασυνείδητα ,η δεν μου είναι εύκολο να εκφράσω τις σκέψεις σε γραπτό λόγο.
 ώστε
ώστε  και
και 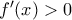 για κάθε
για κάθε  .
.
 ώστε
ώστε  και
και 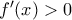 για κάθε
για κάθε  .
.

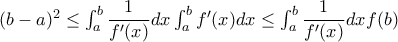





 Τροποποιούμενη δίνει το αποτέλεσμα και χωρίς
Τροποποιούμενη δίνει το αποτέλεσμα και χωρίς  είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα.




 με
με 

 με
με 
 για να πάρω
για να πάρω
 αναμένω ότι
αναμένω ότι  . Εφαρμόζω λοιπόν την Cauchy-Schwarz ως εξής:
. Εφαρμόζω λοιπόν την Cauchy-Schwarz ως εξής:


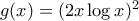 . Τότε
. Τότε  για κάποιο
για κάποιο  .
.  Άρα
Άρα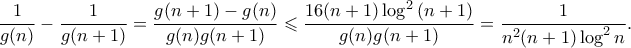





 οπότε το ζητούμενο είναι προφανές.
οπότε το ζητούμενο είναι προφανές.
 έφτιαξα μια ανισότητα μεταξύ των ολοκληρωμάτων.
έφτιαξα μια ανισότητα μεταξύ των ολοκληρωμάτων.