IMC 1995/1/4

#1

Ορίζουμε την συνάρτηση $F:(1,\infty) \to \mathbb{R}$ ως

$\displaystyle{ F(x) = \int_x^{x^2} \frac{\mathrm{d}t}{\ln{t}}}$

Να δειχθεί ότι η

είναι 1-1 και να βρεθεί το πεδίο τιμών της.

Tolaso J Kos · #2

Demetres έγραψε:Ορίζουμε την συνάρτηση $F:(1,\infty) \to \mathbb{R}$ ως

$\displaystyle{ F(x) = \int_x^{x^2} \frac{\mathrm{d}t}{\ln{t}}}$

Να δειχθεί ότι η είναι 1-1 και να βρεθεί το πεδίο τιμών της.

Γεια σου Δημήτρη,

η άσκηση αυτή ταιριάζει ταμάμ στο Λύκειο. Την έχουμε δει εξάλλου πολλές φορές στους σχετικούς φακέλους. Τέλος πάντων. Από το να ψάξω να τη βρω δίδω μία απάντηση.

Εφόσον βρισκόμαστε στο $(1, +\infty)$ η υπό ολοκλήρωση συνάρτηση είναι συνεχής και άρα η ${\rm F}$ είναι παραγωγίσιμη. Για το τυχόν $\alpha \in (1, +\infty)$ έχουμε ότι:
$\displaystyle{\begin{aligned} {\rm F'} (x) &= \left ( \int_{x}^{x^2} \frac{{\rm d}t}{\ln t} \right )' \\ &= \left ( \int_{x}^{\alpha} \frac{{\rm d}t}{\ln t} + \int_{\alpha}^{x^2} \frac{{\rm d}t}{\ln t} \right )'\\ &= \left ( \int_{\alpha}^{x^2} \frac{{\rm d}t}{\ln t} - \int_{\alpha}^{x} \frac{{\rm d}t}{\ln t}\right )'\\ &= \frac{2x}{\ln x^2} - \frac{1}{\ln x}\\ &\!\!\overset{x>1}{=\! =\!} \frac{x}{\ln x} - \frac{1}{\ln x} \\ &= \frac{x-1}{\ln x} >0 \end{aligned}}$ Άρα η ${\rm F}$ είναι γνήσια αύξουσα και κατά συνέπεια 1-1

. Ως γνήσια αύξουσα και συνεχής το σύνολο τιμών που ζητείται είναι ίσο με
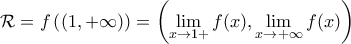$\displaystyle{\mathcal{R}=f\left ( \left ( 1, +\infty \right ) \right )= \left ( \lim_{x\rightarrow 1+} f(x) , \lim_{x\rightarrow +\infty} f(x) \right )}$ Ας υπολογίσουμε το πρώτο όριο το οποίο ως γνωστόν κάνει $\ln 2$ . Βγαίνει με πολλούς τρόπους αλλά ο γρηγορότερος είναι ο εξής. Χρησιμοποιούμε τη διπλή ανισότητα $\displaystyle{1- \frac{1}{x}< \ln x < x- 1}$ για κάθε x >1

. Οπότε:
$\displaystyle{\frac{1}{t-1}< \frac{1}{\ln t}< \frac{t}{t-1}\Rightarrow \int_{x}^{x^2}\frac{{\rm d}t}{t-1}< \int_{x}^{x^2}\frac{{\rm d}t}{\ln t}< \int_{x}^{x^2}\frac{t}{t-1}\, {\rm d}t}$ Παίρνοντας όρια βγάζουμε ότι πράγματι το ζητούμενο όριο είναι ίσο με $\ln 2$ . Πάμε για το $+\infty$ . Εδώ παρατηρούμε πως αφού η

είναι γνήσια αύξουσα θα ισχύει το εξής:
$\displaystyle{{\rm F}(x)> \frac{x^2-x}{\ln x^2} \Rightarrow \lim_{x \rightarrow +\infty} {\rm F}(x) \geq \lim_{x\rightarrow +\infty} \frac{x^2-x}{2\ln x} \overset{\left (\frac{\infty}{\infty} \right )}{=\! =\! =\!}\lim_{x\rightarrow +\infty} \frac{x}{2} \left ( 2x-1 \right ) = +\infty}$ Άρα το ζητούμενο σύνολο τιμών είναι το $\mathcal{R}=\left ( \ln 2 , +\infty \right )$ .

#3

Είναι

$\displaystyle{F'(x)=\frac{x-1}{\ln x}>0~~\forall x>1,}$ οπότε η συνάρτηση είναι γνησίως αύξουσα, άρα $\displaystyle{1-1.}$

Φανερά το σύνολο τιμών της συνάρτησης είναι το

$\displaystyle{(\lim_{x\to 1^+}F(x),\lim_{x\to +\infty}F(x))}$ .

Ολοκληρώνοντας στο διάστημα $\displaystyle{[x,x^2]}$ την ανισότητα

$\displaystyle{\frac{t}{t-1}>\frac{1}{\ln t}>\frac{1}{t-1}~~\forall t>1}$ βρίσκουμε

$\displaystyle{x^2-x+\ln (x+1)>F(x)>\ln (x+1).}$

Από εδώ είναι άμεσο ότι

$\displaystyle{\lim_{x\to 1^+}F(x)=\ln 2,~~\lim_{x\to +\infty}F(x)=+\infty.}$

Άρα $\displaystyle{F((1,+\infty))=(\ln 2, +\infty).}$

IMC 1995/1/4

IMC 1995/1/4

Re: IMC 1995/1/4

Re: IMC 1995/1/4

Μέλη σε σύνδεση