 και υποσύνολα
και υποσύνολα  του
του ![[n] [n]](/forum/ext/geomar/texintegr/latexrender/pictures/de504dafb2a07922de5e25813d0aaafd.png) ώστε
ώστε (α)
![A_1 \cup \cdots \cup A_{k} = [n] A_1 \cup \cdots \cup A_{k} = [n]](/forum/ext/geomar/texintegr/latexrender/pictures/fa8894db7f7e704f3fca92f50a812994.png) ,
,(β)
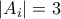 για κάθε
για κάθε ![i \in [k] i \in [k]](/forum/ext/geomar/texintegr/latexrender/pictures/27dd3dfaefefcf386c3f3b080d3634db.png) ,
,(γ) για κάθε δύο
![x,y \in [n] x,y \in [n]](/forum/ext/geomar/texintegr/latexrender/pictures/d4ec5b37f84f0cd9cc43eb5407c5153e.png) με
με  η δυάδα
η δυάδα  ανήκει είτε σε ακριβώς δύο είτε σε κανένα
ανήκει είτε σε ακριβώς δύο είτε σε κανένα  και
και(δ) κάθε
![x \in [n] x \in [n]](/forum/ext/geomar/texintegr/latexrender/pictures/5ac0b6d62b6b36a22d0ad7d2d33aac9e.png) ανήκει σε ακριβώς
ανήκει σε ακριβώς  από τα
από τα  .
.Να βρεθούν όλες οι πιθανές τιμές του
 .
.[Όπου με
![[m] [m]](/forum/ext/geomar/texintegr/latexrender/pictures/efc831aabf9ade051f781ccb54c2dcdb.png) συμβολίζω το σύνολο
συμβολίζω το σύνολο  .]
.]Συντονιστής: Demetres
 και υποσύνολα
και υποσύνολα  του
του ![[n] [n]](/forum/ext/geomar/texintegr/latexrender/pictures/de504dafb2a07922de5e25813d0aaafd.png) ώστε
ώστε ![A_1 \cup \cdots \cup A_{k} = [n] A_1 \cup \cdots \cup A_{k} = [n]](/forum/ext/geomar/texintegr/latexrender/pictures/fa8894db7f7e704f3fca92f50a812994.png) ,
,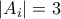 για κάθε
για κάθε ![i \in [k] i \in [k]](/forum/ext/geomar/texintegr/latexrender/pictures/27dd3dfaefefcf386c3f3b080d3634db.png) ,
,![x,y \in [n] x,y \in [n]](/forum/ext/geomar/texintegr/latexrender/pictures/d4ec5b37f84f0cd9cc43eb5407c5153e.png) με
με  η δυάδα
η δυάδα  ανήκει είτε σε ακριβώς δύο είτε σε κανένα
ανήκει είτε σε ακριβώς δύο είτε σε κανένα  και
και![x \in [n] x \in [n]](/forum/ext/geomar/texintegr/latexrender/pictures/5ac0b6d62b6b36a22d0ad7d2d33aac9e.png) ανήκει σε ακριβώς
ανήκει σε ακριβώς  από τα
από τα  .
. .
.![[m] [m]](/forum/ext/geomar/texintegr/latexrender/pictures/efc831aabf9ade051f781ccb54c2dcdb.png) συμβολίζω το σύνολο
συμβολίζω το σύνολο  .]
.] ,στη δεύτερη του
,στη δεύτερη του  κ.ό.κ.
κ.ό.κ. .
.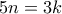 .
. δυάδες.
δυάδες. .
. .
. ικανοποιείται ο ισχυρισμός του προβλήματος.
ικανοποιείται ο ισχυρισμός του προβλήματος.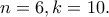 Τα υποσύνολα
Τα υποσύνολα  ικανοποιούν τον ισχυρισμό του προβλήματος.
ικανοποιούν τον ισχυρισμό του προβλήματος.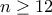 ,τοποθετούμε τα πρώτα 6 στοιχεία του [n] στις 10 πρώτες στήλες του πίνακα όπως παραπάνω,τα επόμενα 6 στις επόμενες 10 στήλες με τον ίδιο τρόπο κ.ο.κ.
,τοποθετούμε τα πρώτα 6 στοιχεία του [n] στις 10 πρώτες στήλες του πίνακα όπως παραπάνω,τα επόμενα 6 στις επόμενες 10 στήλες με τον ίδιο τρόπο κ.ο.κ. .
.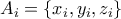 θεωρούμε ένα «αφηρημένο» τρίγωνο
θεωρούμε ένα «αφηρημένο» τρίγωνο  . Αν δυο τρίγωνα έχουν κοινή πλευρά τότε τα κολλάμε μεταξύ τους. Οι συνθήκες (α)-(γ) μας λένε πως έχουμε μια τριγωνοποίηση με
. Αν δυο τρίγωνα έχουν κοινή πλευρά τότε τα κολλάμε μεταξύ τους. Οι συνθήκες (α)-(γ) μας λένε πως έχουμε μια τριγωνοποίηση με  κορυφές μιας κλειστής επιφάνειας
κορυφές μιας κλειστής επιφάνειας  . Η επιφάνεια έχει
. Η επιφάνεια έχει  κορυφές και
κορυφές και 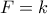 έδρες. Επίσης αφού κάθε ακμή ανήκει σε ακριβώς δύο έδρες και κάθε έδρα έχει ακριβώς
έδρες. Επίσης αφού κάθε ακμή ανήκει σε ακριβώς δύο έδρες και κάθε έδρα έχει ακριβώς  ακμές παίρνουμε ότι
ακμές παίρνουμε ότι  . Τέλος με τον ίδιο τρόπο από την συνθήκη (δ) παίρνουμε
. Τέλος με τον ίδιο τρόπο από την συνθήκη (δ) παίρνουμε 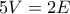 .
. και άρα
και άρα 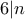 .
. 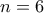 ψάχνουμε για μια τριγωνοποίηση (με έξι κορυφές) μιας επιφάνειας με χαρακτηριστική
ψάχνουμε για μια τριγωνοποίηση (με έξι κορυφές) μιας επιφάνειας με χαρακτηριστική  . Οπότε ψάχνουμε για τριγωνοποίηση του πραγματικού προβολικού επιπέδου (real projective plane).
. Οπότε ψάχνουμε για τριγωνοποίηση του πραγματικού προβολικού επιπέδου (real projective plane).  απλά
απλά  ξένες μεταξύ τους τριγωνοποιήσεις όπως πιο πάνω.
ξένες μεταξύ τους τριγωνοποιήσεις όπως πιο πάνω.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες