 , όπου
, όπου  και
και  ο
ο  οστός αριθμός Fibonacci.
οστός αριθμός Fibonacci.Συντονιστής: Demetres
 , όπου
, όπου  και
και  ο
ο  οστός αριθμός Fibonacci.
οστός αριθμός Fibonacci.Κοτρώνης Αναστάσιος έγραψε: ↑Δευ Σεπ 17, 2012 8:30 pmΥπολογίστε το άθροισμα, όπου
και
ο
οστός αριθμός Fibonacci.
 . Το ζητούμενο άθροισμα είναι η τιμή
. Το ζητούμενο άθροισμα είναι η τιμή 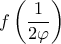 . Ξεκινάμε από τη γεννήτρια των αριθμών Fibonacci η οποία είναι:
. Ξεκινάμε από τη γεννήτρια των αριθμών Fibonacci η οποία είναι:





Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες