 . Να υπολογιστεί το
. Να υπολογιστεί το  .
.Συντονιστής: Demetres
 . Να υπολογιστεί το
. Να υπολογιστεί το  .
.
 διαφορετικά μονοπάτια από το
διαφορετικά μονοπάτια από το  στο
στο  μέσω του
μέσω του 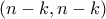 όπου κάθε φορά μετακινούμαστε ένα βήμα δεξιά ή ένα βήμα πάνω.
όπου κάθε φορά μετακινούμαστε ένα βήμα δεξιά ή ένα βήμα πάνω.
 ως το
ως το  πόσες φορές περάσαμε από ένα από τα σημεία
πόσες φορές περάσαμε από ένα από τα σημεία  .
.  μονοπάτια περνάμε από το
μονοπάτια περνάμε από το  θα υπολογίσουμε το
θα υπολογίσουμε το  το οποίο μετράει πόσες φορές περάσαμε από ένα από τα σημεία
το οποίο μετράει πόσες φορές περάσαμε από ένα από τα σημεία  .
.  μετράει για όλα τα μονοπάτια από το
μετράει για όλα τα μονοπάτια από το  ως το
ως το  πόσες φορές περάσαμε από ένα από τα σημεία
πόσες φορές περάσαμε από ένα από τα σημεία  .
.  επομένως το ζητούμενο άθροισμα θα είναι
επομένως το ζητούμενο άθροισμα θα είναι ![\displaystyle S_n = \frac{1}{2}\left[16^n + \binom{2n}{n}^2 \right] \displaystyle S_n = \frac{1}{2}\left[16^n + \binom{2n}{n}^2 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/9ad0f9fae97d0ee0ad8fe35cb5a1d13b.png)
 το πρώτο σημείο μετά το
το πρώτο σημείο μετά το  στην κύρια διαγώνιο από το οποίο περνάμε. Υπάρχουν
στην κύρια διαγώνιο από το οποίο περνάμε. Υπάρχουν 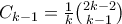 τρόπο να πάμε από το
τρόπο να πάμε από το  στο
στο  μένοντας αυστηρά κάτω από τη διαγώνιο (εκτός από το πρώτο και τελευταίο σημείο). Επίσης για να πάμε από το
μένοντας αυστηρά κάτω από τη διαγώνιο (εκτός από το πρώτο και τελευταίο σημείο). Επίσης για να πάμε από το  στο
στο  επαγωγικά περνάμε
επαγωγικά περνάμε  φορές από σημεία της κύριας διαγωνίου.
φορές από σημεία της κύριας διαγωνίου.
 στο αριστερό μέλος το βάλαμε διότι μπορούμε να πάμε από το
στο αριστερό μέλος το βάλαμε διότι μπορούμε να πάμε από το  στο
στο  μένοντας αυστηρά κάτω ή αυστηρά πάνω από τη διαγώνιο. Επίσης το
μένοντας αυστηρά κάτω ή αυστηρά πάνω από τη διαγώνιο. Επίσης το  στο δεξί μέλος υπάρχει επειδή δεν μετρήσαμε πόσες φορές περάσαμε από το
στο δεξί μέλος υπάρχει επειδή δεν μετρήσαμε πόσες φορές περάσαμε από το  . Δηλαδή πόσα είναι τα συνολικά μονοπάτια.
. Δηλαδή πόσα είναι τα συνολικά μονοπάτια. με το
με το  να είναι άμεσο. Για το επαγωγικό βήμα παρατηρούμε ότι
να είναι άμεσο. Για το επαγωγικό βήμα παρατηρούμε ότι 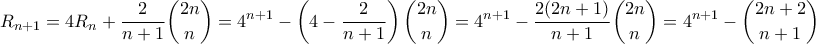
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες