 (!) φοιτητές, εκ των οποίων οι
(!) φοιτητές, εκ των οποίων οι  διαγωνίστηκαν δια ζώσης.
διαγωνίστηκαν δια ζώσης.Να σημειωθεί ότι λόγω του αυξημένου αριθμού των συμμετεχόντων χωρίς αρχηγό, το βάρος ανά διορθωτή ήταν ιδιαίτερα αυξημένο και όπως πληροφορηθήκαμε από τους διοργανωτές τα αποτελέσματα για τους εξ αποστάσεως συμμετέχοντες μπορεί να αργήσουν ακόμα και μερικές μέρες. Από την Ελλάδα συμμετείχαν δια ζώσης ομάδες από τη Θεσσαλονίκη και την Πάτρα, ενώ υπήρχαν και φοιτητές από Θεσσαλονίκη, Αθήνα και Πάτρα που συμμετείχαν διαδικτυακά.
Μιας και πλέον έχουν αναρτηθεί τα θέματα στην επίσημη ιστοσελίδα του διαγωνισμού, τα παραθέτω και εδώ για συζήτηση.
Μέρα 1
Πρόβλημα 1: Έστω ολοκληρώσιμη συνάρτηση
![f:[0,1]\rightarrow (0, \infty) f:[0,1]\rightarrow (0, \infty)](/forum/ext/geomar/texintegr/latexrender/pictures/274e0d74cc6958c99afb2853c711b096.png) τέτοια ώστε
τέτοια ώστε 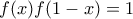 για κάθε
για κάθε ![x \in [0,1] x \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c75c22c0876976bad2957525698cc870.png) . Να δειχθεί ότι
. Να δειχθεί ότι 
Πρόβλημα 2: Έστω
 θετικός ακέραιος. Να βρεθούν όλοι οι
θετικός ακέραιος. Να βρεθούν όλοι οι  πραγματικοί πίνακες
πραγματικοί πίνακες  με μόνο πραγματικές ιδιοτιμές που ικανοποιούν τη σχέση
με μόνο πραγματικές ιδιοτιμές που ικανοποιούν τη σχέση  για κάποιον ακέραιο
για κάποιον ακέραιο 
Πρόβλημα 3: Έστω
 πρώτος αριθμός. Ένας ψύλλος στέκεται στο σημείο
πρώτος αριθμός. Ένας ψύλλος στέκεται στο σημείο  του πραγματικού άξονα. Κάθε λεπτό ο ψύλλος έχει τις εξής δυνατότητες: να μείνει στη θέση του, να κινηθεί κατά 1 αριστερά ή κατά 1 δεξιά. Μετά από
του πραγματικού άξονα. Κάθε λεπτό ο ψύλλος έχει τις εξής δυνατότητες: να μείνει στη θέση του, να κινηθεί κατά 1 αριστερά ή κατά 1 δεξιά. Μετά από  λεπτά ο ψύλλος θέλει να βρίσκεται ξανά στο
λεπτά ο ψύλλος θέλει να βρίσκεται ξανά στο  . Έστω
. Έστω  ο αριθμός των τρόπων να το κάνει αυτό. Να βρεθεί το
ο αριθμός των τρόπων να το κάνει αυτό. Να βρεθεί το  modulo
modulo  (Για παράδειγμα για
(Για παράδειγμα για  : είτε δεν κουνιέται από τη θέση του, είτε πάει αριστερά και μετά δεξιά, είτε δεξιά και μετά αριστερά)
: είτε δεν κουνιέται από τη θέση του, είτε πάει αριστερά και μετά δεξιά, είτε δεξιά και μετά αριστερά)Πρόβλημα 4: Έστω
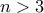 ακέραιος. Έστω
ακέραιος. Έστω  το σύνολο όλων των μη διατεταγμένων τριάδων με διακριτά στοιχεία από το σύνολο
το σύνολο όλων των μη διατεταγμένων τριάδων με διακριτά στοιχεία από το σύνολο  . Έστω
. Έστω  ο ελάχιστος αριθμός χρωμάτων που αρκούν για να χρωματίσουμε τα στοιχεία του
ο ελάχιστος αριθμός χρωμάτων που αρκούν για να χρωματίσουμε τα στοιχεία του  , έτσι ώστε, αν
, έτσι ώστε, αν  , οι τριάδες
, οι τριάδες  και
και  να έχουν διαφορετικά χρώματα. Να δειχθεί ότι
να έχουν διαφορετικά χρώματα. Να δειχθεί ότι 
Μέρα 2
Πρόβλημα 5: Χρωματίζουμε όλες τις πλευρές και τις διαγωνίους ενός κανονικού πολυγώνου
 με
με  γωνίες είτε μπλε είτε κόκκινες, έτσι ώστε από κάθε κορυφή του πολυγώνου να είναι άκρο
γωνίες είτε μπλε είτε κόκκινες, έτσι ώστε από κάθε κορυφή του πολυγώνου να είναι άκρο  κόκκινων και
κόκκινων και 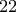 μπλε τμημάτων. Ένα τρίγωνο που σχηματίζεται από κορυφές του
μπλε τμημάτων. Ένα τρίγωνο που σχηματίζεται από κορυφές του  λέγεται μονοχρωματικό αν όλες οι πλευρές του έχουν το ίδιο χρώμα. Υποθέτουμε ότι υπάρχουν
λέγεται μονοχρωματικό αν όλες οι πλευρές του έχουν το ίδιο χρώμα. Υποθέτουμε ότι υπάρχουν  μονοχρωματικά μπλε τρίγωνα. Πόσα μονοχρωματικά κόκκινα τρίγωνα υπάρχουν;
μονοχρωματικά μπλε τρίγωνα. Πόσα μονοχρωματικά κόκκινα τρίγωνα υπάρχουν;Πρόβλημα 6: Έστω
 πρώτος αριθμός. Να δειχθεί ότι υπάρχει μετάθεση
πρώτος αριθμός. Να δειχθεί ότι υπάρχει μετάθεση  του
του  τέτοια ώστε
τέτοια ώστε 
Πρόβλημα 7: Έστω
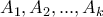 ταυτοδύναμοι πραγματικοί
ταυτοδύναμοι πραγματικοί  πίνακες τέτοιοι ώστε
πίνακες τέτοιοι ώστε  για κάθε
για κάθε 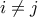 . Να δειχθεί ότι τουλάχιστον ένας από τους πίνακες έχει
. Να δειχθεί ότι τουλάχιστον ένας από τους πίνακες έχει 
Πρόβλημα 8: Έστω
 ακέραιοι και έστω
ακέραιοι και έστω  ένας κύκλος. Επιλέγουμε
ένας κύκλος. Επιλέγουμε  μπλε και
μπλε και  κόκκινα σημεία ομοιόμορφα και ανεξάρτητα τυχαία πάνω στον κύκλο
κόκκινα σημεία ομοιόμορφα και ανεξάρτητα τυχαία πάνω στον κύκλο  . Έστω
. Έστω  η τομή του κυρτού καλύμματος των κόκκινων σημείων και του κυρτού καλύμματος των μπλε σημείων. Έστω
η τομή του κυρτού καλύμματος των κόκκινων σημείων και του κυρτού καλύμματος των μπλε σημείων. Έστω  ο αριθμός των κορυφών του κυρτού πολυγώνου
ο αριθμός των κορυφών του κυρτού πολυγώνου  (συγκεκριμένα
(συγκεκριμένα  όταν το
όταν το  είναι κενό). Να βρεθεί η μέση τιμή του
είναι κενό). Να βρεθεί η μέση τιμή του  .
.
 . Σπάμε το αρχικό ολοκλήρωμα και εργαζόμαστε με αλλαγή μεταβλητής:
. Σπάμε το αρχικό ολοκλήρωμα και εργαζόμαστε με αλλαγή μεταβλητής: .
. θετική) έχουμε
θετική) έχουμε ![f(x)+f(1-x)\geq 2\sqrt{f(x)f(1-x)}=2 ,\forall x\in[0,\frac{1}{2}] f(x)+f(1-x)\geq 2\sqrt{f(x)f(1-x)}=2 ,\forall x\in[0,\frac{1}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/8e73257a773489f1aada0ec276edef5e.png) .
. όπως έπρεπε.
όπως έπρεπε.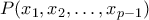 το υπόλοιπο του αθροίσματος
το υπόλοιπο του αθροίσματος  modulo
modulo 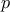 .
. ορίζουμε το υπόλοιπο που προκύπτει από μια αρχική μετάθεση αν εναλλάξουμε τα
ορίζουμε το υπόλοιπο που προκύπτει από μια αρχική μετάθεση αν εναλλάξουμε τα  και
και  στοιχεία.
στοιχεία. την ταυτοτικη μετάθεση των στοιχείων.
την ταυτοτικη μετάθεση των στοιχείων.


 :
:
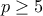
 και άρα
και άρα 
 .
. :
:
 εφόσον
εφόσον  στην μετάθεση Α.
στην μετάθεση Α. εκτελούμε τις εξής πράξεις διαδοχικά:
εκτελούμε τις εξής πράξεις διαδοχικά:
 φορές και τελικά καταλήγουμε σε υπόλοιπο
φορές και τελικά καταλήγουμε σε υπόλοιπο  .
. :
:
 ξεκινώντας από το Α μειώνουμε το υπόλοιπο κατά
ξεκινώντας από το Α μειώνουμε το υπόλοιπο κατά  απο την ιδιότητα 2.
απο την ιδιότητα 2. είναι
είναι 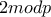 οπότε εκτελούμε
οπότε εκτελούμε  ακόμα πράξεις τύπου (1) (Αν
ακόμα πράξεις τύπου (1) (Αν  ) ως εξής:
) ως εξής: (2)
(2) (1)
(1)
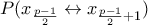
 όπου δουλεύουν οι μεταθέσεις
όπου δουλεύουν οι μεταθέσεις  αντίστοιχα.
αντίστοιχα.
 ισχύει
ισχύει  και αντικαθιστώντας τη δοθείσα έχουμε
και αντικαθιστώντας τη δοθείσα έχουμε 
 του πίνακα
του πίνακα 
 . Προφανώς
. Προφανώς 
 ισχύει
ισχύει 
 άρτιος οπότε ανεξάρτητα από το πρόσημο του
άρτιος οπότε ανεξάρτητα από το πρόσημο του 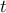 ισχύει
ισχύει  και το ζητούμενο έπεται. Αν
και το ζητούμενο έπεται. Αν  άρτιος το ζητούμενο είναι πάλι προφανές, αφού
άρτιος το ζητούμενο είναι πάλι προφανές, αφού 
 είναι η
είναι η 
 για κάποιο
για κάποιο 
 αφού από Cayley-Hamilton ισχύει
αφού από Cayley-Hamilton ισχύει 
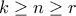 ισχύει προφανώς
ισχύει προφανώς  και άρα αντικαθιστώντας στη δοθείσα παίρνουμε
και άρα αντικαθιστώντας στη δοθείσα παίρνουμε  , άρα ο
, άρα ο  , όπου
, όπου 


 από τα αριστερά και με
από τα αριστερά και με  από τα δεξιά και αξιοποιώντας την ιδιότητα ότι
από τα δεξιά και αξιοποιώντας την ιδιότητα ότι  προκύπτει ότι
προκύπτει ότι  ή ισοδύναμα θέτοντας
ή ισοδύναμα θέτοντας  έχουμε
έχουμε 
 το ελάχιστο πολυώνυμο του πίνακα
το ελάχιστο πολυώνυμο του πίνακα 

 άρα
άρα 

 , οπότε πρέπει όλες οι ιδιοτιμές του
, οπότε πρέπει όλες οι ιδιοτιμές του  και άρα από Cayley-Hamilton
και άρα από Cayley-Hamilton  δηλαδή
δηλαδή 
 .
.  υπάρχει μια στήλη του
υπάρχει μια στήλη του  , τέτοια ώστε
, τέτοια ώστε  .
. 
 -διάστατα διανύσματα
-διάστατα διανύσματα  είναι γραμμικά ανεξάρτητα από όπου το ζητούμενο έπεται άμεσα.
είναι γραμμικά ανεξάρτητα από όπου το ζητούμενο έπεται άμεσα.
 από αριστερά έχουμε
από αριστερά έχουμε 
 -οστού είναι της μορφής
-οστού είναι της μορφής  άρα πρέπει να είναι
άρα πρέπει να είναι 
 και αφού
και αφού  προκύπτει
προκύπτει 
 άρα όλοι οι πίνακες διαγωνιοποιούνται ταυτόχρονα από την ίδια βάση ιδιοδιανυσμάτων.
άρα όλοι οι πίνακες διαγωνιοποιούνται ταυτόχρονα από την ίδια βάση ιδιοδιανυσμάτων. ο πίνακας που διαγωνιοποιεί τους
ο πίνακας που διαγωνιοποιεί τους  άρα
άρα 


 που είναι ακριβώς το πλήθος των άσσων στη διαγώνιο του
που είναι ακριβώς το πλήθος των άσσων στη διαγώνιο του  έχει
έχει  άσσους στη διαγώνιο και τα υπόλοιπα στοιχεία του είναι
άσσους στη διαγώνιο και τα υπόλοιπα στοιχεία του είναι  έχει
έχει  άσσους στη διαγώνιο. Όμως για να ισχύει
άσσους στη διαγώνιο. Όμως για να ισχύει  πρέπει ο
πρέπει ο 

 θα πρέπει να έχει
θα πρέπει να έχει 

 τότε καταλήγουμε ότι
τότε καταλήγουμε ότι  , άτοπο
, άτοπο
 πρέπει να είναι ο πίνακας με τη ζητούμενη ιδιότητα. Προφανώς οι ιδιότητες είναι συμμετρικές και ανεξάρτητες της σειράς των πινάκων οπότε οποιοσδήποτε (αλλά τουλάχιστον ένας) από τους πίνακες μπορεί (πρέπει) να έχει την ζητούμενη ιδιότητα.
πρέπει να είναι ο πίνακας με τη ζητούμενη ιδιότητα. Προφανώς οι ιδιότητες είναι συμμετρικές και ανεξάρτητες της σειράς των πινάκων οπότε οποιοσδήποτε (αλλά τουλάχιστον ένας) από τους πίνακες μπορεί (πρέπει) να έχει την ζητούμενη ιδιότητα.