Για ποιους ακεραίους
 είναι ο αριθμός
είναι ο αριθμός  πρώτος;
πρώτος;ΘΕΜΑ 2
Να βρεθεί η μέγιστη τιμή της πραγματικής σταθερής
 έτσι ώστε
έτσι ώστε 
για όλους τους θετικούς πραγματικούς αριθμούς
 για τους οποίους
για τους οποίους 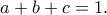
ΘΕΜΑ 3
Έστω τρίγωνο
 ,
, 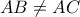 , και
, και  το έκκεντρό του.
το έκκεντρό του. Ο εγγεγραμμένος κύκλος του τριγώνου εφάπτεται της πλευράς
 στο σημείο
στο σημείο  .
. Αν
 το μέσο της
το μέσο της  , να αποδείξετε ότι η ευθεία
, να αποδείξετε ότι η ευθεία 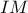 περνάει από το μέσο του τμήματος
περνάει από το μέσο του τμήματος  .
.ΘΕΜΑ 4
Σε ένα καλοκαιρινό σχολείο παραδίδονται
 μαθήματα. Κάθε μαθητής παρακολούθησε τουλάχιστον ένα μάθημα και κάθε μάθημα παρακολουθήθηκε από τουλάχιστον
μαθήματα. Κάθε μαθητής παρακολούθησε τουλάχιστον ένα μάθημα και κάθε μάθημα παρακολουθήθηκε από τουλάχιστον  μαθητές. Γνωρίζουμε ότι για κάθε δύο μαθήματα υπάρχουν το πολύ
μαθητές. Γνωρίζουμε ότι για κάθε δύο μαθήματα υπάρχουν το πολύ  μαθητές οι οποίοι παρακολούθησαν και τα δύο.
μαθητές οι οποίοι παρακολούθησαν και τα δύο. Να δειχθεί ότι στο σχολείο έλαβαν μέρος τουλάχιστον
 μαθητές.
μαθητές.
 μια πέμπτη ριζά της μονάδας τότε
μια πέμπτη ριζά της μονάδας τότε 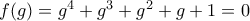 οπότε
οπότε 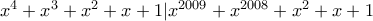
 επειδή θέλουμε
επειδή θέλουμε 
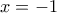 που απορρίπτεται) θα πρέπει
που απορρίπτεται) θα πρέπει  όμως για
όμως για  ,
,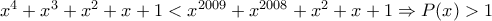 .
.
 .
. ισχύει.
ισχύει. Οπότε αρκεί να δείξουμε ότι:
Οπότε αρκεί να δείξουμε ότι:
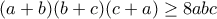 αρκεί να δείξουμε ότι:
αρκεί να δείξουμε ότι: 
 ,
, ,
, τότε η προηγουμένη γράφεται:
τότε η προηγουμένη γράφεται:
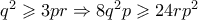 και
και 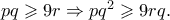
 το αντιδιαμετρικο του
το αντιδιαμετρικο του  είναι συνευθειακα.
είναι συνευθειακα. η
η 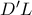 πηγαίνοντας τώρα στο
πηγαίνοντας τώρα στο  έχουμε το ζητούμενο.
έχουμε το ζητούμενο. ο μιγαδικός του
ο μιγαδικός του 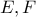 οι επαφές του κύκλου με τις
οι επαφές του κύκλου με τις  και
και  οι αντίστοιχοι μιγαδικοί τους. Ας είναι
οι αντίστοιχοι μιγαδικοί τους. Ας είναι 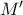 το μέσο της
το μέσο της 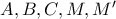 έχουμε:
έχουμε:
 .
.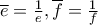 , λόγω μοναδιαίου κύκλου.
, λόγω μοναδιαίου κύκλου.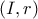 ο εγγεγραμμένος και
ο εγγεγραμμένος και  ο παρεγγεγραμμένος στην πλευρά
ο παρεγγεγραμμένος στην πλευρά  στην πλευρά
στην πλευρά  και στις προεκτάσεις των
και στις προεκτάσεις των  .
. το πρώτο σημείο που η
το πρώτο σημείο που η  συναντά τον
συναντά τον  που απεικονίζει τον
που απεικονίζει τον  άρα και το
άρα και το  κι αφού το
κι αφού το  θα είναι και
θα είναι και  , συνεπώς το
, συνεπώς το  , είναι :
, είναι :  . Δηλαδή τα
. Δηλαδή τα  είναι μέσα των
είναι μέσα των  .
. διέρχεται κι από το μέσο , έστω
διέρχεται κι από το μέσο , έστω  , του
, του