 με
με  όπου
όπου  πραγματικοί αριθμοί. Να αποδείξετε ότι δεν υπάρχουν ακέραιοι αριθμοί
πραγματικοί αριθμοί. Να αποδείξετε ότι δεν υπάρχουν ακέραιοι αριθμοί  , τέτοιοι ώστε
, τέτοιοι ώστε και
και 
Πρόβλημα 2: Δίνεται τρίγωνο
 εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  . Στο εσωτερικό των τμημάτων
. Στο εσωτερικό των τμημάτων  και
και  παίρνουμε σημεία
παίρνουμε σημεία  και
και  αντίστοιχα. Οι παράλληλες από τα σημεία
αντίστοιχα. Οι παράλληλες από τα σημεία  και
και  προς την
προς την  τέμνουν τον κύκλο
τέμνουν τον κύκλο  για δεύτερη φορά στα σημεία
για δεύτερη φορά στα σημεία  και
και  αντίστοιχα. Έστω
αντίστοιχα. Έστω  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών  και
και  . Οι κάθετες ευθείες από το
. Οι κάθετες ευθείες από το  προς τις
προς τις  και
και  τέμνουν τις ευθείες
τέμνουν τις ευθείες  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα.
αντίστοιχα. Αν η ευθεία
 τέμνει την
τέμνει την  στο σημείο
στο σημείο  , να αποδείξετε ότι η
, να αποδείξετε ότι η  είναι κάθετη στη
είναι κάθετη στη  .
.Πρόβλημα 3: Έστω
 το πλήθος των τρόπων με τους οποίους μπορούμε να καλύψουμε μια
το πλήθος των τρόπων με τους οποίους μπορούμε να καλύψουμε μια  σκακιέρα (
σκακιέρα ( γραμμές και
γραμμές και 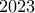 στήλες) χρησιμοποιώντας τα παρακάτω πλακίδια:
στήλες) χρησιμοποιώντας τα παρακάτω πλακίδια:Να βρείτε τα δύο τελευταία ψηφία του
 .
.Σημείωση: Κάθε πλακίδιο καλύπτει ακριβώς τρία τετραγωνάκια της σκακιέρας και μπορεί να τοποθετηθεί μόνο όπως φαίνεται παραπάνω. Π.χ.\ το πρώτο από τα παραπάνω πλακίδια μπορεί να τοποθετηθεί μόνο κάθετα και όχι οριζόντια.
Πρόβλημα 4: Να αποδείξετε ότι υπάρχει πεπερασμένο πλήθος φυσικών αριθμών
 που ικανοποιούν τη σχέση
που ικανοποιούν τη σχέση
Σημείωση: Με
 συμβολίζουμε το πλήθος των θετικών διαιρετών του
συμβολίζουμε το πλήθος των θετικών διαιρετών του  (συμπεριλαμβανομένων των
(συμπεριλαμβανομένων των  και
και  ) και με
) και με  το πλήθος των θετικών ακεραίων μικρότερων ή ίσων του
το πλήθος των θετικών ακεραίων μικρότερων ή ίσων του  που είναι σχετικά πρώτοι ως προς τον
που είναι σχετικά πρώτοι ως προς τον  .
.
 , ισοδύναμα θέλω το σύνολο
, ισοδύναμα θέλω το σύνολο  των θετικών ακεραίων με
των θετικών ακεραίων με  να είναι πεπερασμένο,
να είναι πεπερασμένο,  πρώτος θα έπρεπε
πρώτος θα έπρεπε 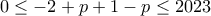 το οποίο είναι αδύνατο, άρα στο
το οποίο είναι αδύνατο, άρα στο  , θα έπρεπε
, θα έπρεπε  το οποίο είναι αδύνατο για μεγάλα
το οποίο είναι αδύνατο για μεγάλα  , άρα κοιτάμε τα μεγάλα στοιχεία του
, άρα κοιτάμε τα μεγάλα στοιχεία του  .
. , έστω
, έστω  τότε
τότε 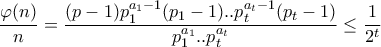
 ώστε
ώστε  για άπειρα
για άπειρα 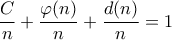 και επομένως
και επομένως 
 , και έτσι για τα μεγάλα
, και έτσι για τα μεγάλα  αφού όμως
αφού όμως  αυτό σημαίνει ότι τα μεγάλα
αυτό σημαίνει ότι τα μεγάλα  είναι δηλαδή δυνάμεις πρώτων, τότε όμως
είναι δηλαδή δυνάμεις πρώτων, τότε όμως  η οποία όμως είναι απλό να δούμε ότι δεν έχει άπειρες λύσεις.
η οποία όμως είναι απλό να δούμε ότι δεν έχει άπειρες λύσεις.![d(n)\geq \sqrt[3]{n} d(n)\geq \sqrt[3]{n}](/forum/ext/geomar/texintegr/latexrender/pictures/2d1771fa02c615c52753426bdd170767.png) ισχύει για πεπερασμένο πλήθος αριθμών
ισχύει για πεπερασμένο πλήθος αριθμών  αρκεί να δείξουμε ότι :
αρκεί να δείξουμε ότι : ισχύει για πεπερασμένο πλήθος αριθμών
ισχύει για πεπερασμένο πλήθος αριθμών 

 ,
,

 ισχύει για πεπερασμένο πλήθος αριθμών
ισχύει για πεπερασμένο πλήθος αριθμών  τότε
τότε  και
και  .
. τότε
τότε  και
και  ώστε να μην υπάρχει
ώστε να μην υπάρχει  φυσικος τέτοιος ώστε
φυσικος τέτοιος ώστε ![d(n)\leq \sqrt[3]{n} d(n)\leq \sqrt[3]{n}](/forum/ext/geomar/texintegr/latexrender/pictures/86e15eef8a3f3587b76ef09cd958f296.png) για κάθε
για κάθε 
 .
. με
με  και
και  τότε:
τότε:
![n-2023\leq d(n)+\phi(n)\leq n-\sqrt{n}+\sqrt[3]{n}\Rightarrow \sqrt{n}\leq \sqrt[3]{n}+2023 n-2023\leq d(n)+\phi(n)\leq n-\sqrt{n}+\sqrt[3]{n}\Rightarrow \sqrt{n}\leq \sqrt[3]{n}+2023](/forum/ext/geomar/texintegr/latexrender/pictures/4365711b0c477d5d934eda5952105a28.png) που ισχύει.
που ισχύει. το πλήθος των τροπών για να καλύψουμε μια
το πλήθος των τροπών για να καλύψουμε μια  με
με  ,
,



 τότε επειδή
τότε επειδή  έχουμε
έχουμε  οπότε:
οπότε:

 και
και 
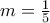 , που δεν είναι ακέραιος
, που δεν είναι ακέραιος
 , που δεν είναι ακέραιος
, που δεν είναι ακέραιος αντί των
αντί των 

![\Leftrightarrow a[(6m-1)^2-m^2]+b[(6m-1)-m]=0 \Leftrightarrow a[(6m-1)^2-m^2]+b[(6m-1)-m]=0](/forum/ext/geomar/texintegr/latexrender/pictures/ffb008d2b54d5d279a2e46d7e893ee15.png)
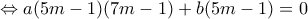
![\Leftrightarrow (5m-1)[a(7m-1)+b]=0 \Leftrightarrow (5m-1)[a(7m-1)+b]=0](/forum/ext/geomar/texintegr/latexrender/pictures/3aebadaccb8ada2fe3f65344d42b19ec.png)
 , διότι
, διότι 


![\Leftrightarrow a[(3-15n)^2-n^2]+b[(3-15n)-n]=0 \Leftrightarrow a[(3-15n)^2-n^2]+b[(3-15n)-n]=0](/forum/ext/geomar/texintegr/latexrender/pictures/9e2c36084763cec2784f22ed3616375e.png)

![\Leftrightarrow (3-16n)[a(3-14n)+b]=0 \Leftrightarrow (3-16n)[a(3-14n)+b]=0](/forum/ext/geomar/texintegr/latexrender/pictures/fa5dc91b305e03849330a948f4f9e3f6.png)
 , διότι
, διότι 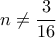
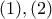 προκύπτει ότι
προκύπτει ότι  .
. τότε και
τότε και  άρα
άρα  , σταθερό, άτοπο.
, σταθερό, άτοπο. , άτοπο.
, άτοπο. ώστε να ικανοποιούνται οι παραπάνω συνθήκες.
ώστε να ικανοποιούνται οι παραπάνω συνθήκες.
 Οπότε
Οπότε 
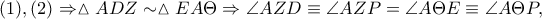 άρα
άρα  εγγράψιμο, δηλαδή τα σημεία
εγγράψιμο, δηλαδή τα σημεία  είναι ομοκυκλικά. Επομένως
είναι ομοκυκλικά. Επομένως 

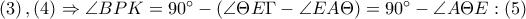

 άρα θα είναι και
άρα θα είναι και  έτσι η
έτσι η 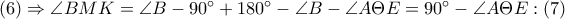
 και
και  όπως θέλαμε
όπως θέλαμε